Question

6．已知函数$f（x）={x^2}-3\left|x\right|+\frac{1}{4}（x∈R）$
（1）判断函数的奇偶性；
（2）画出函数的图象；
（3）指数函数的单调区间．

Answer 1

分析 （1）根据奇偶性的定义即可判断，
（2）函数配方得f（x）=（|x|-$\frac{3}{2}$）²-2，作出函数的图象如图所示，
（3）由图象直接可得答案．

解答 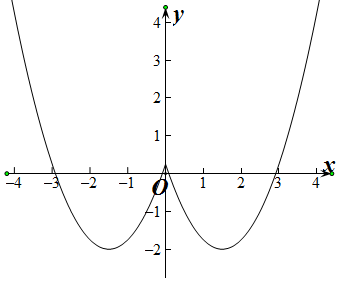解：（1）函数的定义域为R，
由于f（-x）=（-x）²-3|-x|+$\frac{1}{4}$=x²-3|x|+$\frac{1}{4}$=f（x），
所以函数为偶函数，
（2）函数配方得f（x）=（|x|-$\frac{3}{2}$）²-2，作出函数的图象如图所示：
（3）由函数的图象可得，函数的单调递增区间是[-$\frac{3}{2}$，0]，[$\frac{3}{2}$，+∞），
函数的单调递减区间是（-∞，$\frac{3}{2}$），[0，$\frac{3}{2}$]，

点评 本题考查了函数的图象和识别，关键时掌握图象的画法，属于基础题．