
分析 (1)根据绝对值不等式|a+b|≥|a-b|便可得出|x+3|+|x-1|≥4,从而得出f(x)的最小值为4,即得到t=4;
(2)利用柯西不等式即可证明.
解答 (1)解f(x)=|x-5|+|x-3|≥|(x-5)-(x-3)|=2;
∴f(x)的最小值m为2;
(2)证明:∵a>0,b>0,$\frac{1}{a}$+$\frac{1}{b}$=$\sqrt{3}$,
∴($\frac{1}{{a}^{2}}$+$\frac{2}{{b}^{2}}$)[${1}^{2}+(\frac{1}{\sqrt{2}})^{2}$]≥$(\frac{1}{a}×1+\frac{\sqrt{2}}{b}×\frac{1}{\sqrt{2}})^{2}$=3≥2.
点评 考查绝对值不等式公式:|a|+|b|≥|a-b|,以及柯西不等式的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x-1,g(x)=$\frac{{x}^{2}}{x}$-1 | B. | f(x)=|x|,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=1,g(x)=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)={x^2}-3\left|x\right|+\frac{1}{4}(x∈R)$
已知函数$f(x)={x^2}-3\left|x\right|+\frac{1}{4}(x∈R)$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
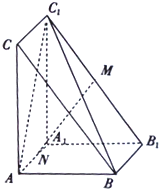 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1、AA1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1、AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com