
���� ��1��������APΪֱ����Բ������ԲC���ҽ���F���ɵ�$\overrightarrow{PF}$•$\overrightarrow{AF}$=c��c-$\frac{8}{3}$��+$\frac{1}{3}$b2=0���ѵ�P��$\frac{8}{3}$��$\frac{b}{3}$��������Բ�ķ���Ϊ$\frac{64}{9{a}^{2}}$+$\frac{1}{9}$=1����b2+c2=a2����������ɵó�a��b�������õ���Բ���̣�
��2������ֱ��l��б�ʲ����ںʹ��ڣ����ֱ�߷��̣�������Բ���̣�����Τ�ﶨ�����ҳ���ʽ����б�ʵĹ�ʽ������ɵ�t2=2+4k2�����ɵ㵽ֱ�ߵľ��빫ʽ�����ɵõ���OBC�����Ϊ��ֵ��
��� �⣺��1��A��0��b����
����APΪֱ����Բ������ԲC���ҽ���F����PF��AF��
��$\overrightarrow{PF}$•$\overrightarrow{AF}$=��c-$\frac{8}{3}$��-$\frac{b}{3}$��•��c��-b��=c��c-$\frac{8}{3}$��+$\frac{1}{3}$b2=0��
�ѵ�P��$\frac{8}{3}$��$\frac{b}{3}$��������ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1�ķ���Ϊ��$\frac{64}{9{a}^{2}}$+$\frac{1}{9}$=1��
���a2=8����b2+c2=8��
�ɵ�b2=8-c2������c��c-$\frac{8}{3}$��+$\frac{1}{3}$b2=0�����c=2��b=2��
����ԲE�ķ���Ϊ$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1��
��2��֤������ֱ��l��б�ʲ����ڣ���x=m��������Բ���̣�
�ɵ�y=��2$\sqrt{1-\frac{{m}^{2}}{8}}$����kOB•kOC=-$\frac{1}{2}$���ɵ�$\frac{-4��1-\frac{{m}^{2}}{8}��}{{m}^{2}}$=-$\frac{1}{2}$��
���m=��2��������2����$\sqrt{2}$����-2����$\sqrt{2}$����
���С�OBC�����Ϊ$\frac{1}{2}$��2��2$\sqrt{2}$=2$\sqrt{2}$��
��б�ʴ���ʱ����ֱ��l�ķ���Ϊy=kx+t��������Բ����x2+2y2=8��
�ɵã�1+2k2��x2+4ktx+2t2-8=0��
��B��x1��y1����C��x2��y2������x1+x2=-$\frac{4kt}{1+2{k}^{2}}$��x1x2=$\frac{2{t}^{2}-8}{1+2{k}^{2}}$��
|x1-x2|=$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{\frac{16{k}^{2}{t}^{2}}{��1+2{k}^{2}��^{2}}-\frac{8{t}^{2}-32}{1+2{k}^{2}}}$=$\frac{2\sqrt{8+16{k}^{2}-2{t}^{2}}}{1+2{k}^{2}}$��
��kOB•kOC=-$\frac{1}{2}$���ɵ�$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$��
��Ϊx1x2+2y1y2=0����y1=kx1+t��y2=kx2+t��
�ɵã�1+2k2��x1x2+2kt��x1+x2��+2t2=0��
���У�1+2k2��•$\frac{2{t}^{2}-8}{1+2{k}^{2}}$+2kt��-$\frac{4kt}{1+2{k}^{2}}$��+2t2=0��
����ɵã�t2=2+4k2��
����|x1-x2|=$\frac{4\sqrt{2{t}^{2}}}{{t}^{2}}$=$\frac{4\sqrt{2}}{|t|}$��
ԭ�㵽ֱ��y=kx+t�ľ���Ϊd=$\frac{|t|}{\sqrt{1+{k}^{2}}}$��
�ɵá�OBC�����ΪS=$\frac{1}{2}$d|BC|
=$\frac{1}{2}$•$\frac{|t|}{\sqrt{1+{k}^{2}}}$•$\sqrt{1+{k}^{2}}$•$\frac{4\sqrt{2}}{|t|}$=2$\sqrt{2}$��
���ǿɵá�OBC�����Ϊ��ֵ2$\sqrt{2}$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ�ҳ����⡢�㵽ֱ�ߵľ��빫ʽ�������ε������ʽ�����ã�������������������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-2��1��0} | B�� | {-2��-1��0��1��2} | C�� | {-1��0} | D�� | {-2��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
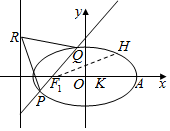 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������������PQR�Ķ���R��C������l�ϣ�P��Q����Բ�ϣ����߶�PQ������F1��KPQ=1��
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������������PQR�Ķ���R��C������l�ϣ�P��Q����Բ�ϣ����߶�PQ������F1��KPQ=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 3016 | B�� | 3020 | C�� | 3024 | D�� | 3028 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com