练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．满足约束条件|x|+2|y|≤2的目标函数z=y-x的最大值为2．

    分析 作出不等式组对应的平面区域，利用目标函数的几何意义，进行求最值即可．

    解答 解：由z=y-x得y=x+z，
    作出不等式组对应的平面区域如图（阴影部分）：
    平移直线y=x+z由图象可知当直线y=x+z经过点A（-2，0）时，直线y=x+z的截距最大，
    此时z也最大，
    代入目标函数z=0-（-2）=2，
    即目标函数的最大值为2，
    故答案为：2．

    点评 本题主要考查线性规划的应用，利用数形结合是解决线性规划问题中的基本方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．若直线x=m（m＞1）与函数f（x）=logax，g（x）=logbx的图象及x轴分别交于A，B，C三点，若$\overrightarrow{AB}$=2$\overrightarrow{BC}$，则（　　）
    A．b=a2B．a=b2C．b=a3D．a=b3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．对于函数f（x）给出定义：
    设f′（x）是函数y=f（x）的导数，f″（x）是函数f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．
    某同学经过探究发现：任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．给定函数$f（x）=\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}+3x-\frac{5}{12}$，请你根据上面探究结果，计算
    $f（\frac{1}{2017}）+f（\frac{2}{2017}）+f（\frac{3}{2017}）+…+f（\frac{2016}{2017}）$=2016．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

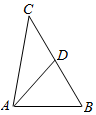    7．已知在△ABC中，角A，B，C所对的边分别为a，b，c．若∠ABC=$\frac{π}{3}$，b=$\sqrt{7}$，c=2，D为BC的中点．
    （Ⅰ）求cos∠BAC的值；
    （Ⅱ）求AD的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数$f（x）=|{x-a}|+|{x-\frac{1}{2}}|，x∈R$
    （Ⅰ）当$a=\frac{5}{2}$时，解不等式f（x）≤x+10；
    （Ⅱ）关于x的不等式f（x）≥a在R上恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

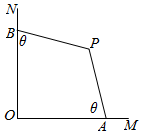    4．某菜农有两段总长度为20米的篱笆PA及PB，现打算用它们和两面成直角的墙OM、ON围成一个如图所示的四边形菜园OAPB（假设OM、ON这两面墙都足够长）．已知|PA|=|PB|=10（米），∠AOP=∠BOP=$\frac{π}{4}$，∠OAP=∠OBP．设∠OAP=θ，四边形OAPB的面积为S．
    （1）将S表示为θ的函数，并写出自变量θ的取值范围；
    （2）求出S的最大值，并指出此时所对应θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知点A为椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的上顶点，P（$\frac{8}{3}$，$\frac{b}{3}$）是椭圆E上的一点，以AP为直径的圆经过椭圆E的右焦点F，直线l与椭圆相交于B、C两点，且满足kOB•kOC=-$\frac{1}{2}$，O为坐标原点
    （1）求椭圆E的方程；
    （2）求证：△OBC的面积为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知tanα=3，则sinαsin（$\frac{3π}{2}$-α）的值是-$\frac{3}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知f（x）=x2-alnx，a∈R．
    （1）讨论函数f（x）的单调性；
    （2）当a＞0时，若f（x）的最小值为1，求a的值；
    （3）设g（x）=f（x）-2x，若g（x）有两个极值点x1，x2（x1＜x2），证明：g（x1）+g（x2）＞-$\frac{5}{2}$．

    查看答案和解析>>

    同步练习册答案