
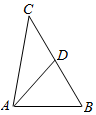
 已知在△ABC中,角A,B,C所对的边分别为a,b,c.若∠ABC=$\frac{π}{3}$,b=$\sqrt{7}$,c=2,D为BC的中点.
已知在△ABC中,角A,B,C所对的边分别为a,b,c.若∠ABC=$\frac{π}{3}$,b=$\sqrt{7}$,c=2,D为BC的中点.分析 (I)法1:由已知及正弦定理可求sinC,利用大边对大角可得C为锐角,利用同角三角函数基本关系式可求cosC,由三角形内角和定理及两角和的余弦函数公式即可求值得解
法2:由余弦定理可求a的值,即可利用余弦定理可求$cos∠BAC=\frac{{A{B^2}+A{C^2}-B{C^2}}}{2AB•AC}$的值.
(II)法1:由$\overrightarrow{AD}=\frac{1}{2}({\overrightarrow{AB}+\overrightarrow{AC}})$,两边平方即可解得AD的值.
法2:在△ABC中,由余弦定理可求BC=3,$BD=\frac{3}{2}$,在△ABD中,由余弦定理得即可解得AD的值;
法3:设E为AC的中点,连结DE,则 $DE=\frac{1}{2}AB=1$,$AE=\frac{1}{2}AC=\frac{1}{2}\sqrt{7}$,在△ADE中,由余弦定理可求AD的值.
解答 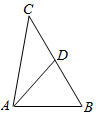 (本题满分为12分)
(本题满分为12分)
解:(I)法1:由正弦定理得$sinC=\frac{c}{b}sinB=\frac{2}{{\sqrt{7}}}×\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{{\sqrt{7}}}$…(1分)
又∵在△ABC中,b>c,∴C<B,∴$0<C<\frac{π}{2}$…(2分)
∴$cosC=\sqrt{1-{{sin}^2}C}=\sqrt{1-\frac{3}{7}}=\frac{2}{{\sqrt{7}}}$…(3分)
∴cos∠BAC=cos(π-B-C)=-cos(B+C)…(4分)
=-(cosBcosC-sinBsinC)…(5分)
=$\frac{{\sqrt{3}}}{2}×\frac{{\sqrt{3}}}{{\sqrt{7}}}-\frac{1}{2}×\frac{2}{{\sqrt{7}}}=\frac{{\sqrt{7}}}{14}$…(6分)
法2:在△ABC中,由余弦定理得AC2=AB2+BC2-2AB•BCcos∠ABC…(1分)
∴$7=4+{a^2}-2×2×a×\frac{1}{2}$,…(2分)
∴(a-3)(a+1)=0解得a=3(a=-1已舍去),…(4分)
∴$cos∠BAC=\frac{{A{B^2}+A{C^2}-B{C^2}}}{2AB•AC}$…(5分)
=$\frac{4+7-9}{{2×2×\sqrt{7}}}=\frac{{\sqrt{7}}}{14}$.…(6分)
(II)法1:∵$\overrightarrow{AD}=\frac{1}{2}({\overrightarrow{AB}+\overrightarrow{AC}})$…(8分)
∴${\overrightarrow{AD}^2}=\frac{1}{4}{({\overrightarrow{AB}+\overrightarrow{AC}})^2}=\frac{1}{4}({{{\overrightarrow{AB}}^2}+{{\overrightarrow{AC}}^2}+2\overrightarrow{AB}•\overrightarrow{AC}})$…(10分)
=$\frac{1}{4}({4+7+2×2×\sqrt{7}×\frac{{\sqrt{7}}}{14}})$=$\frac{13}{4}$…(11分)
∴$AD=\frac{{\sqrt{13}}}{2}$.…(12分)
法2:在△ABC中,由余弦定理得BC2=AB2+AC2-2AB•ACcos∠BAC…(7分)
=$4+7-2×2×\sqrt{7}×\frac{{\sqrt{7}}}{14}=9$,…(8分)
∴BC=3,
∴$BD=\frac{3}{2}$…(9分)
在△ABD中,由余弦定理得 AD2=AB2+BD2-2AB•BD•cos∠ABD,…(10分)
=$4+\frac{9}{4}-2×2×\frac{3}{2}×\frac{1}{2}=\frac{13}{4}$,…(11分)
∴$AD=\frac{{\sqrt{13}}}{2}$,…(12分)
法3:设E为AC的中点,连结DE,则 $DE=\frac{1}{2}AB=1$,…(7分)
$AE=\frac{1}{2}AC=\frac{1}{2}\sqrt{7}$…(8分)
在△ADE中,由余弦定理得AD2=AE2+DE2-2AE•DE•cos∠AED,…(9分)
=$\frac{7}{4}+1+2×\frac{{\sqrt{7}}}{2}×1×\frac{{\sqrt{7}}}{14}=\frac{13}{4}$,…(11分)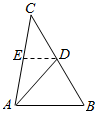
∴$AD=\frac{{\sqrt{13}}}{2}$.…(12分)
点评 本题主要考查了正弦定理,大边对大角,同角三角函数基本关系式,三角形内角和定理,两角和的余弦函数公式,余弦定理,平面向量及其运算在解三角形中的综合应用,考查了计算能力,转化思想和数形结合思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 总计 | |
| 女生 | 15 | ||
| 男生 | 12 | 20 | |
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 3016 | B. | 3020 | C. | 3024 | D. | 3028 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5项 | B. | 6项 | C. | 7项 | D. | 8项 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com