
| A. | 99 | B. | 88 | C. | 77 | D. | 66 |
科目:高中数学 来源: 题型:解答题
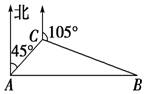 一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.
一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [9,49] | B. | (17,49] | C. | [9,41] | D. | (17,41] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
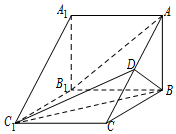 (文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(文科)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com