
 “ª…Ã¥¨––÷¡À˜¬Ì¿Ô∫£”Ú ±£¨‘‚µΩ∫£µ¡µƒ◊∑ª˜£¨Àʺ¥∑¢≥ˆ«Ûæ»–≈∫≈£Æ’˝‘⁄∏√∫£”Ú÷¥––ª§∫Ω»ŒŒÒµƒ∫£æ¸°∞ª∆…Ω°±Ω¢‘⁄A¥¶ªÒœ§∫Û£¨º¥≤‚≥ˆ∏√…Ã¥¨‘⁄∑ΩŒªΩ«Œ™45°„æý¿Î10∫£¿ÔµƒC¥¶£¨≤¢—ÿ∑ΩŒªΩ«Œ™105°„µƒ∑ΩœÚ£¨“‘9∫£¿Ô/ ±µƒÀŸ∂»∫Ω––£Æ°∞ª∆…Ω°±Ω¢¡¢º¥“‘21∫£¿Ô/ ±µƒÀŸ∂»«∞»•”™æ»£Æ»ÁÕºÀ˘ 棨«Û°∞ª∆…Ω°±Ω¢øøΩ¸…Ã¥¨À˘–Ë“™µƒ◊Ó…Ÿ ±º‰º∞À˘æ≠π˝µƒ¬∑≥ãÆ
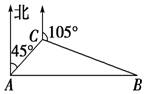
“ª…Ã¥¨––÷¡À˜¬Ì¿Ô∫£”Ú ±£¨‘‚µΩ∫£µ¡µƒ◊∑ª˜£¨Àʺ¥∑¢≥ˆ«Ûæ»–≈∫≈£Æ’˝‘⁄∏√∫£”Ú÷¥––ª§∫Ω»ŒŒÒµƒ∫£æ¸°∞ª∆…Ω°±Ω¢‘⁄A¥¶ªÒœ§∫Û£¨º¥≤‚≥ˆ∏√…Ã¥¨‘⁄∑ΩŒªΩ«Œ™45°„æý¿Î10∫£¿ÔµƒC¥¶£¨≤¢—ÿ∑ΩŒªΩ«Œ™105°„µƒ∑ΩœÚ£¨“‘9∫£¿Ô/ ±µƒÀŸ∂»∫Ω––£Æ°∞ª∆…Ω°±Ω¢¡¢º¥“‘21∫£¿Ô/ ±µƒÀŸ∂»«∞»•”™æ»£Æ»ÁÕºÀ˘ 棨«Û°∞ª∆…Ω°±Ω¢øøΩ¸…Ã¥¨À˘–Ë“™µƒ◊Ó…Ÿ ±º‰º∞À˘æ≠π˝µƒ¬∑≥Ã£Æ ∑÷Œˆ …ËÀ˘–Ë ±º‰Œ™t–° ±£¨‘⁄µ„B¥¶œý”ˆ‘Úø…«Ûµ√AB∫ÕBC£¨Ω¯∂¯¿˚”√”ýœ“∂®¿ÌΩ®¡¢µ» Ω«Ûµ√t£¨¥”∂¯ø…µ√Ω·¬€£Æ
Ω‚¥ Ω‚£∫…ËÀ˘–Ë ±º‰Œ™t–° ±£¨°≠£®1∑÷£©
‘ÚAB=21t£¨BC=9t£Æ°≠£®2∑÷£©
”÷“—÷™AC=10£¨“¿Ã‚“‚÷™£¨°œACB=120°„£¨°≠£®3∑÷£©
∏˘æð”ýœ“∂®¿Ì£¨AB2=AC2+BC2-2•AC•BCcos°œACB£Æ°≠£®5∑÷£©
°ý£®21t£©2=102+£®9t£©2-2°¡10°¡9tcos 120°„£¨°≠£®6∑÷£©
°ý£®21t£©2=100+81t2+90t£¨
º¥360t2-90t-100=0£Æ°≠£®8∑÷£©
°ýt=$\frac{2}{3}$ªÚt=-$\frac{5}{12}$£®…·£©£Æ°≠£®10∑÷£©
°ýAB=21°¡$\frac{2}{3}$=14£®∫£¿Ô£©£Æ°≠£®11∑÷£©
º¥°∞ª∆…Ω°±Ω¢–Ë“™”√$\frac{2}{3}$–° ±øøΩ¸…Ã¥¨£¨π≤∫Ω––14∫£¿Ô£Æ°≠£®12∑÷£©
µ„∆¿ ±æÂ÷˜“™øº≤È¡ÀΩ‚»˝Ω«–Œµƒ µº ”¶”√£¨øº≤È”ýœ“∂®¿Ì£¨ Ù”⁄÷–µµÃ‚£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫Ω‚¥Ã‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | $-\frac{4}{5}$ | B£Æ | $\frac{4}{5}$ | C£Æ | $-\frac{7}{25}$ | D£Æ | $\frac{7}{25}$ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫Ω‚¥Ã‚
| x | °≠ | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | °≠ |
| y | °≠ | 17 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | °≠ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | a°ð$\frac{4}{3}$ | B£Æ | 0£ºa°Ð1 | C£Æ | 1°Ða°Ð$\frac{4}{3}$ | D£Æ | 0£ºa°Ð1ªÚa°ð$\frac{4}{3}$ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 0∏ˆ | B£Æ | 1∏ˆ | C£Æ | 2∏ˆ | D£Æ | 3∏ˆ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 99 | B£Æ | 88 | C£Æ | 77 | D£Æ | 66 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com