
分析 本题利用几何概型求解.先根据到点的距离等于1的点构成图象特征,求出其体积,最后利用体积比即可得点P到点O1,O2的距离都大于1的概率
解答 解:∵到点O1的距离等于1的点构成一个半个球面,到点O2的距离等于1的点构成一个半个球面,两个半球构成一个整球,如图,
点P到点O1,O2的距离都大于1的概率为:
P=$\frac{球外的体积}{圆柱体积}$=$\frac{圆柱体积-球体积}{圆柱体积}$=1-$\frac{\frac{4}{3}π×{1}^{3}}{π×{1}^{2}×2}$=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$
点评 本小题主要考查几何概型、圆柱和球的体积等基础知识,考查运算求解能力,考查空间想象力、化归与转化思想.关键是明确满足题意的测度为体积比.


科目:高中数学 来源: 题型:解答题
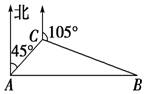 一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.
一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{85}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [9,49] | B. | (17,49] | C. | [9,41] | D. | (17,41] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com