
| A. | a≥$\frac{4}{3}$ | B. | 0<a≤1 | C. | 1≤a≤$\frac{4}{3}$ | D. | 0<a≤1或a≥$\frac{4}{3}$ |
分析 本题考查的是简单线性规划问题.线性规划要注意数形结合,要综合运用多方面的知识.特别要注意区域的边界.因此在解答此题时应先根据先行约束条件画出可行域,然后根据可行域的特点及条件:表示的平面区域是一个三角形及其内部,找出不等关系即可.
解答 解:由题意可知:画可行域如图:
不等式组表示的平面区域是一个三角形及其内部,
且当直线x+y=a过直线y=x与直线2x+y=2的交点时,a=$\frac{4}{3}$.
所以a的取值范围是:0<a≤1或a≥$\frac{4}{3}$,
故选:D.
点评 本题考查的是简单线性规划问题.在解答的过程当中成分体现了数形结合的思想和构成三角形的相关知识.特别是对线性规划中的区域边界考查得到了充分的体现.值得同学们体会反思.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
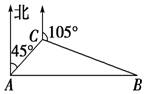 一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.
一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{85}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com