
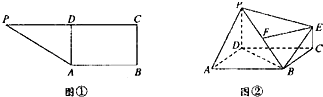
分析 (1)连接AC与BD交于点F′,则F′为BD的中点,连接FF′,证明AC⊥PD,FE∥AC,即可证明PD⊥EF;
(2)若PD=4,利用分割法求多面体ABCDPE的体积.
解答 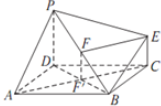 (1)证明:连接AC与BD交于点F′,则F′为BD的中点,连接FF′,
(1)证明:连接AC与BD交于点F′,则F′为BD的中点,连接FF′,
∵PF=BF,DF′=BF′,
∴FF′∥PD∥EC.
∵$EC=\frac{1}{2}PD$,FF′=$\frac{1}{2}PD$,
∴FF′=EC,
∴FF′CE为平行四边形,
∴FE∥F′C,
∴FE∥AC.
∵PD⊥AD,PD⊥DC,AD∩DC=D,
∴PD⊥平面ABCD.
∵AC?平面ABCD,
∴AC⊥PD,
∵FE∥AC,
∴FE⊥PD.
(2)解:由题意,VABCDPE=VP-ABD+VB-CEPD=$\frac{1}{3}×4×(\frac{1}{2}×4×4)$+$\frac{1}{3}×4×[\frac{1}{2}(2+4)×4]$=$\frac{32}{3}+\frac{48}{3}$=$\frac{80}{3}$.
点评 本题考查线面垂直,线线垂直,考查体积的计算,考查学生分析解决问题的能力,难度中等.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
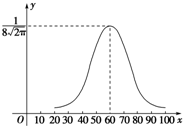 某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.
某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com