练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．在以点O为圆心，1为半径的半圆弧上任取一点B，如图，则△AOB的面积大于＜“m“：math xmlns：dsi='http://www．dessci．com/uri/2003/MathML'dsi：zoomscale='150'dsi：_mathzoomed='1'style='CURSOR：pointer； DISPLAY：inline-block'＞14$\frac{1}{4}$的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{1}{2}$D．$\frac{3}{4}$

    分析 利用OA=1，△AOB的面积大于$\frac{1}{4}$，可得$\frac{π}{6}$＜∠AOB＜$\frac{5π}{6}$，即可求出△AOB的面积大于$\frac{1}{4}$的概率．

    解答 解：∵OA=1，△AOB的面积大于$\frac{1}{4}$，
    ∴$\frac{1}{2}×1×1×sin∠AOB＞\frac{1}{4}$，
    ∴sin∠AOB＞$\frac{1}{2}$，
    ∴$\frac{π}{6}$＜∠AOB＜$\frac{5π}{6}$，
    ∴△AOB的面积大于$\frac{1}{4}$的概率为$\frac{2}{3}$．
    故选：B．

    点评 本题考查△AOB的面积大于$\frac{1}{4}$的概率，确定$\frac{π}{6}$＜∠AOB＜$\frac{5π}{6}$是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．若函数f（x）=lnx-ax在区间（1，+∞）上是单调减函数，则a的取值范围是$\underline{[{1，+∞}）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．在△ABC中，tanA=$\frac{3}{4}$，tan（A-B）=-$\frac{1}{3}$，则tanC的值为$\frac{79}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．以下角：①异面直线所成角；②直线和平面所成角；③二面角的平面角，可能为钝角的有1个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知偶函数f（x）的定义域为R，且在（-∞，0）上是增函数，则f（a2-a+1）与f（$\frac{3}{4}$）的大小关系为（　　）
    A．f（a2-a+1）＜$f（\frac{3}{4}）$B．f（a2-a+1）＞$f（\frac{3}{4}）$C．f（a2-a+1）≤$f（\frac{3}{4}）$D．f（a2-a+1）≥$f（\frac{3}{4}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设函数f（x）=|2x+2|-|x-2|．
    （1）求不等式f（x）＜0的解集；
    （2）若?x∈R，f（x）+t3+2t≥0恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如表统计表，其中“√”表示购买，“×”表示未购买．
    顾客人数/商品甲乙丙丁
    100√×√√
    217×√×√
    200√√√×
    300√×√×
    85√×××
    98×√××
    （1）估计顾客同时购买乙和丙的概率；
    （2）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；
    （3）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中那种商品的可能性最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

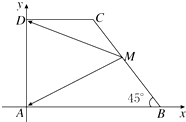    8．在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B=45°，AB=2CD=4，M为腰BC的中点，则$\overrightarrow{MA}$•$\overrightarrow{MD}$=（　　）
    A．10B．8C．6D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．数列1$\frac{1}{2}$，4$\frac{1}{4}$，9$\frac{1}{8}$，16$\frac{1}{16}$…，前n项之和为（　　）
    A．$\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1+\frac{1}{{2}^{n}}$B．$\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$-$\frac{1}{{2}^{n}}$
    C．$\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$+$\frac{1}{{2}^{n-1}}$D．$\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$-$\frac{1}{{2}^{n-1}}$

    查看答案和解析>>

    同步练习册答案