练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知圆C：x2＋y2－4x－6y＋12＝0，点A(3,5)，求：

    (1)过点A的圆的切线方程；

    (2)O点是坐标原点，连接OA，OC，求△AOC的面积S.


    解：(1)⊙C：(x－2)2＋(y－3)2＝1.

    当切线的斜率不存在时，有直线x＝3，C(2,3)到直线的距离为1，满足条件．

    当切线的斜率存在时，设直线y－5＝k(x－3)，即y＝kx＋5－3k，＝1，解得k＝.

    ∴直线方程为x＝3或y＝x＋.

    (2)|AO|＝＝，

    lAO：5x－3y＝0，点C到直线OA的距离d＝，

    S△AOC＝d|AO|＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某学校为了了解学生的日平均睡眠时间(单位：h)，随机选择了n名同学进行调查．下表是这n名同学的日睡眠时间的频率分布表：

    序号(i)

    分组(睡眠时间)

    频数(人数)

    频率

     1

    [4,5)

    6

    0.12

    2

    [5,6)

     

    0.20

    3

    [6,7)

    a

    4

    [7,8)

    b

    5

    [8,9)

     

    0.08

    (1)求n的值；若a＝20，将表中数据补全，并画出频率分布直方图；

    (2)统计方法中，同一组数据常用该组区间的中点值(例如区间[4,5)的中点值是4.5)作为代表．若据此计算的上述数据的平均值为6.52，求a，b的值，并由此估计该学校学生的日平均睡眠时间在7小时以上的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则＝(　　)

    A．2                              B．4

    C．5                              D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若两直线y＝x＋2a和y＝2x＋a＋1的交点为P，P在圆x2＋y2＝4的内部，则a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设两圆C1、C2都和两坐标轴相切，且都过点，则两圆心的距离|C1C2|＝(　　)

    A．4                               B．4

    C．8                               D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆C经过点A(－2,0)，B(0,2)，且圆心C在直线y＝x上，又直线l：y＝kx＋1与圆C相交于P、Q两点．

    (1)求圆C的方程；

    (2)若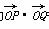＝－2，求实数k的值；

    (3)过点(0,1)作直线l1与l垂直，且直线l1与圆C交于M、N两点，求四边形PMQN面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


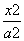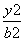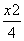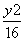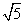    已知双曲线C1：－＝1(a＞0，b＞0)与双曲线C2：－＝1有相同的渐近线，且C1的右焦点为F(，0)，则a＝________，b＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆C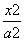：＋＝1(a＞b＞0)的一个顶点为A(2,0)，离心率为.直线y＝k(x－1)与椭圆C交于不同的两点M，N.

    (1)求椭圆C的方程；

    (2)当△AMN的面积为时，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    斜率为1的直线l与椭圆＋y2＝1相交于A、B两点，则|AB|的最大值为(　　)

    A．2                              B.

    C.                          D.

    查看答案和解析>>

    同步练习册答案