练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．sin22°30′•cos22°30′的值为（　　）
    A．$\frac{\sqrt{2}}{2}$B．$\frac{\sqrt{2}}{4}$C．-$\frac{\sqrt{2}}{2}$D．$\frac{1}{2}$

    分析 根据题意，将原式恒等变形可得sin22°30′•cos22°30′=$\frac{1}{2}$（2sin22°30′•cos22°30′）=$\frac{1}{2}$sin（2×22°30′）=$\frac{1}{2}$sin45°，由特殊角的三角函数值计算可得答案．

    解答 解：根据题意，sin22°30′•cos22°30′=$\frac{1}{2}$（2sin22°30′•cos22°30′）=$\frac{1}{2}$sin（2×22°30′）=$\frac{1}{2}$sin45°=$\frac{\sqrt{2}}{4}$；
    故选：B．

    点评 本题考查正弦的二倍角公式，解题的关键是熟悉二倍角公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．已知△ABC的内角A，B，C的对边分别为a，b，c，若$\sqrt{3}$acosC+（$\sqrt{3}$c-2b）cosA=0，且cosA•cosC=$\frac{\sqrt{3}}{4}$，则△ABC是（　　）
    A．直角三角形B．等腰三角形
    C．等边三角形D．等腰三角形或直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知随机变量ξ服从正态分布N（1，1），若P（ξ＜3）=0.977，则P（-1＜ξ＜3）=0.954．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若角α的正弦线的长度为$\frac{3}{4}$，且方向与y轴的正方向相反，则sinα的值为-$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在△ABC中，A，B，C的对边分别是a，b，c，3sin2C+8sin2A=11sinA•sinC，且c＜2a．
    （1）求证：△ABC为等腰三角形
    （2）若△ABC的面积为8$\sqrt{15}$．且sinB=$\frac{\sqrt{15}}{4}$，求BC边上的中线长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．设函数f（x）满足$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{x}$=-1，则f′（1）=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．若$\overrightarrow{AB}$=（-2，5），B（1，-3），则A点的坐标为（3，-8）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．-90°+k•360°（k∈z）表示的是（　　）
    A．第一象限角B．第三象限角C．界限角D．第四象限角

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

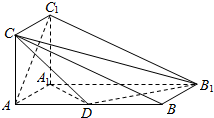    10．如图，三棱柱ABC-A1B1C1的侧面AA1C1C是矩形，侧面AA1C1C⊥侧面AA1B1B，且AB=4AA1=4，∠BAA1=60°，D是AB的中点．
    （Ⅰ）求证：AC1∥平面CDB1；
    （Ⅱ）求证：DA1⊥平面AA1C1C．

    查看答案和解析>>

    同步练习册答案