
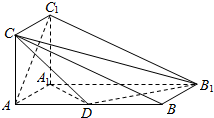
 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.分析 (1)连结A1C交AC1于F,取B1C中点E,连结DE,EF.则可利用中位线定理证明四边形ADEF是平行四边形,得出AF∥CD,从而证明AC1∥平面CDB1.
(2)求出AA1和AD的长,使用余弦定理求出A1D,由勾股定理的逆定理证出A1D⊥AA1,由面面垂直可得出AC⊥平面ABB1A1,进而得出AC⊥A1D,得出DA1⊥平面AA1C1C.
解答 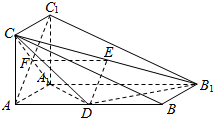 证明:(1)连结A1C交AC1于F,取B1C中点E,连结DE,EF.
证明:(1)连结A1C交AC1于F,取B1C中点E,连结DE,EF.
∵四边形AA1C1C是矩形,∴F是A1C的中点,
∴EF∥A1B1,EF=$\frac{1}{2}$A1B1,
∵四边形ABB1A1是平行四边形,D是AB的中点,
∴AD∥A1B1,AD=$\frac{1}{2}$A1B1,
∴四边形ADEF是平行四边形,∴AF∥DE,即AC1∥DE.
又∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(2)∵AB=4AA1=4,D是AB中点,∴AA1=1,AD=2,
∵∠BAA1=60°,∴A1D=$\sqrt{A{D}^{2}+A{{A}_{1}}^{2}-2AD•A{A}_{1}cos60°}$=$\sqrt{3}$.
∴AA12+A1D2=AD2,∴A1D⊥AA1,
∵侧面AA1C1C⊥侧面AA1B1B,侧面AA1C1C∩侧面AA1B1B=AA1,AC⊥AA1,AC?平面AA1C1C,
∴AC⊥平面AA1B1B,∵A1D?平面AA1B1B,
∴AC⊥A1D,又∵AA1?平面AA1C1C,AC?平面AA1C1C,AC∩AA1=A,
∴DA1⊥平面AA1C1C.
点评 本题考查了线面平行,线面垂直的判断,面面垂直的性质,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\sqrt{3}$(1+$\sqrt{2}$+$\sqrt{3}$) | C. | 3+3$\sqrt{2}$ | D. | 3+3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+3 | B. | -a+5 | C. | a-5 | D. | -a-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,且至少经过一个样本点 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{10}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [-$\sqrt{2}$,-1]∪[$\sqrt{2}$,$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com