
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,且至少经过一个样本点 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
分析 A.根据否命题的定义进行判断.
B.根据线性回归方程的性质进行判断.
C.根据含有量词的命题的否定进行判断.
D.根据逆否命题的等价性进行判断.
解答 解:A.命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”故A错误,
B.线性回归直线方程y=bx+a恒过样本中心$(\overline x,\overline y)$,但不一定过样本点,故B错误,
C.命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1≥0”,故C错误,
D.若x=y,则sinx=siny成立,即原命题成立,则命题的逆否命题为真命题,故D正确,
故选:D
点评 本题主要考查命题的真假判断,涉及四种命题的关系,含有量词的命题的否定,以及线性回归直线方程的性质,比较基础.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
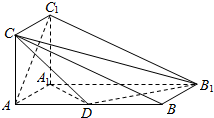 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
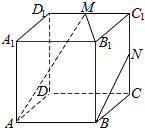
| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,$\frac{25}{3}$] | C. | [$\frac{25}{3}$,+∞) | D. | [9,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com