
| A. | [$\sqrt{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [-$\sqrt{2}$,-1]∪[$\sqrt{2}$,$\sqrt{3}$] |
分析 根据反函数的性质求出a+b=4,然后根据函数奇偶性的性质求出函数f(x)的解析式,判断函数的单调性,利用参数分离法将不等式进行转化进行求解即可.
解答 解:由程x+lgx=4得lgx=4-x,
由x+10x=4得10x=4-x,
记f(x)=lgx,则其反函数f-1(x)=10x,
它们的图象关于直线y=x轴对称,
根据题意,a,b为f(x),f-1(x)的图象与直线y=4-x交点A,B的横坐标,
由于两交A,B点关于直线y=x对称,
所以,B点的横坐标β就是A点的纵坐标,即A(a,b),
将A(a,b)代入直线y=4-x得,a+b=4,
则当x≥0时,f(x)=x2+(a+b-4)x=x2,
∵函数f(x)是定义在R上的奇函数,
∴若x<0,则-x>0,
则f(-x)=x2=-f(x),
即f(x)=-x2,x<0,
则f(x)=$\left\{\begin{array}{l}{{x}^{2},}&{x≥0}\\{-{x}^{2},}&{x<0}\end{array}\right.$,
则函数f(x)在(-∞,+∞)上为增函数,
若对任意x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,
即若对任意x∈[t,t+2],不等式f(x+t)≥f($\sqrt{2}$x)恒成立,
则x+t≥$\sqrt{2}$x恒成立,
则t≥($\sqrt{2}$-1)x,
则x≤$\frac{t}{\sqrt{2}-1}$=($\sqrt{2}$+1)t,
∵x∈[t,t+2],
∴t+2≤($\sqrt{2}$+1)t,
即2≤$\sqrt{2}$t
则t≥$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
故选:A
点评 本题主要考查不等式恒成立问题,根据反函数的性质求出a+b=4,求出函数的解析式,利用参数分离法进行求解是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
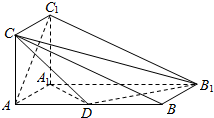 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
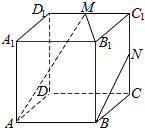
| A. | 直线MN与DC1互相垂直 | B. | 直线AM与BN互相平行 | ||
| C. | 直线MN与BC1所成角为90° | D. | 直线MN垂直于平面A1BCD1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 4 | C. | -7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,$\frac{25}{3}$] | C. | [$\frac{25}{3}$,+∞) | D. | [9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-1 | B. | y=1 | C. | y=-2 | D. | y=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
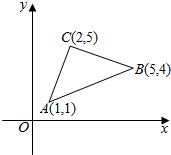 如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.
如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com