
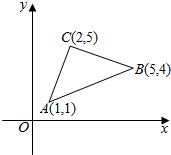
 如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.
如图,已知A(1,1),B(5,4),C(2,5),设向量$\overrightarrow{a}$是与向量$\overrightarrow{AB}$垂直的单位向量.分析 (1)设$\overrightarrow{a}$=(x,y),根据向量的数量积和向量的模得到$\left\{\begin{array}{l}{4x+3y=0}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,解方程得,
(2)设向量$\overrightarrow{AC}$与向量$\overrightarrow{a}$的夹角为θ,在$\overrightarrow{a}$上的投影为h,根据向量的投影即可求出.
(3)根据三角形的面积公式即可求出.
解答 解:(1)设$\overrightarrow{a}$=(x,y),依题意有,
$\overrightarrow{AB}$=(4,3),|$\overrightarrow{AB}$|=5,|$\overrightarrow{a}$|=1,$\overrightarrow{a}$⊥$\overrightarrow{AB}$,即$\overrightarrow{a}•\overrightarrow{AB}$=0,
有$\left\{\begin{array}{l}{4x+3y=0}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{3}{5}}\\{y=\frac{4}{5}}\end{array}\right.$,或${\;}_{\;}^{\;}$$\left\{\begin{array}{l}{x=\frac{3}{5}}\\{y=-\frac{4}{5}}\end{array}\right.$,
所以,$\overrightarrow{a}$=(-$\frac{3}{5}$,$\frac{4}{5}$)或$\overrightarrow{a}$=($\frac{3}{5}$,-$\frac{4}{5}$),
(2)设向量$\overrightarrow{AC}$与向量$\overrightarrow{a}$的夹角为θ,在$\overrightarrow{a}$上的投影为h,
则h=|$\overrightarrow{AC}$|cosθ=$\frac{\overrightarrow{AC}•\overrightarrow{a}}{|\overrightarrow{a}|}$=$\overrightarrow{AC}$•$\overrightarrow{a}$,$\overrightarrow{AC}$=(1,4),
当$\overrightarrow{a}$=(-$\frac{3}{5}$,$\frac{4}{5}$)时,h=1×(-$\frac{3}{5}$)+4×$\frac{4}{5}$=$\frac{13}{5}$,
当$\overrightarrow{a}$=($\frac{3}{5}$,-$\frac{4}{5}$)时,h=1×$\frac{3}{5}$+4×(-$\frac{4}{5}$)=-$\frac{13}{5}$,
(3)S△ABC=$\frac{1}{2}$|$\overrightarrow{AB}$||h|=$\frac{1}{2}$×5×$\frac{13}{5}$=$\frac{13}{2}$.
点评 本题考查了向量的数量积运算和向量的模的计算,以及向量的投影和三角形的面积.


科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [-$\sqrt{2}$,-1]∪[$\sqrt{2}$,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则a-c>b-d | B. | 若a>b,c>d,则ac>bd | ||
| C. | 若$\frac{1}{a}$<$\frac{1}{b}$<0,则ab<b2 | D. | 若$\frac{b}{a}$>$\frac{b-1}{a-1}$,则a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=1(y≠0) | B. | x2+y2=4(y≠0) | C. | x2+y2=9(y≠0) | D. | x2+y2=a2(y≠0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com