
分析 (1)利用三角函数的图象和性质,求得2x+$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],即可求得函数的最大值与最小值;
(2)将原函数转换为y=-sin2x+2sinx-1,将其看成关于t的一元二次函数,写出t的取值范围,根据二次函数的性质求得值域;
(3)将原函数转换f(t)=t2+at+1,t∈[0,1],讨论对称轴的取值,根据二次函数性质求出a的值.
解答 解:(1)y=3-4cos(2x+$\frac{π}{3}$),x∈[-$\frac{π}{3}$,$\frac{π}{6}$],
2x+$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
∴当2x+$\frac{π}{3}$=0时取最小值,最小值为-1,即x=-$\frac{π}{6}$,
2x+$\frac{π}{3}$=$\frac{2π}{3}$时取最大值,最大值为5,即x=$\frac{π}{6}$,
∴x=-$\frac{π}{6}$时,y取最小值为-1,
x=$\frac{π}{6}$时,y取最大值为5;
(2)y=cos2x+2sinx-2,
=-sin2x+2sinx-1,
令sinx=t,t∈[-1,1],
∴y=-t2+2t-1,t∈[-1,1],
由二次函数图象可知,对称轴为1,
∴y在定义域[-1,1]上单调递增,
y的值域为[-4,0],
∴函数y=cos2x+2sinx-2,x∈R的值域[-4,0];
(3)f(x)=-sin2x+acosx+2,x∈[0,$\frac{π}{2}$],
∴f(x)=cos2x+acosx+1,x∈[0,$\frac{π}{2}$],
令cosx=t,t∈[0,1],
∴f(t)=t2+at+1,t∈[0,1],
由二次函数性质可知:a<0,
当对称轴t=-$\frac{a}{2}$>1,即a<-2时,
∴最小值为f(1)=$\frac{1}{2}$,
∴a=$-\frac{3}{2}$>-2,不成立,
当0-$\frac{a}{2}$≤1,-2≤a≤0,
当t=-$\frac{a}{2}$取最小值,
∴a=-2.
点评 本题考查三角函数图象与性质与一元二次函数结合,属于中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{14}{3}$,$\frac{37}{3}$] | B. | [$\frac{1}{3}$,$\frac{50}{3}$] | C. | [$\frac{11}{3}$,6] | D. | [$\frac{41}{6}$,$\frac{22}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
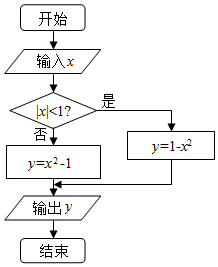 如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.
如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 12 | C. | 54 | D. | 81 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com