
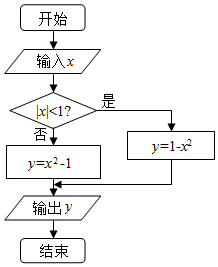
 如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.
如图所示是某函数f(x)给出x的值时,求相应函数y的程序框图.分析 (1)根据程序框图,得出该程序运行后输出的函数f(x)的解析式;
(2)根据f(x)的解析式,画出函数的图象,结合图象即可得出满足条件的x1与x2的取值范围.
解答 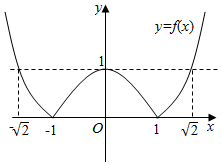 解:(1)根据程序框图,得;
解:(1)根据程序框图,得;
该程序运行后输出的是函数f(x)=$\left\{\begin{array}{l}{1{-x}^{2},|x|<1}\\{{x}^{2}-1,|x|≥1}\end{array}\right.$;
(2)根据f(x)的解析式,画出函数的图象,如图所示;
当输入的x取x1和x2(|x1|<|x2|)时,输出的y值相同,
x1的取值范围是(-1,1),
x2的取值范围是[-$\sqrt{2}$,-1)∪(1,$\sqrt{2}$].
点评 本题考查了程序框图与分段函数的应用问题,也考查了根据函数解析式求对应自变量取值范围的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | sin(α+β)=cosαsinβ+sinαcosβ | B. | cos(α+β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαsinβ-sinαcosβ | D. | cos(α-β)=cosαcosβ-sinαsinβ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
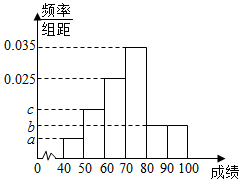 已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.
已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
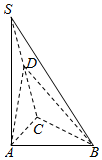 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
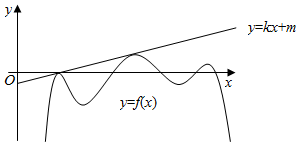
| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第二、四象限 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com