
| A. | -$\frac{{1+\sqrt{3}}}{4}$i | B. | -$\frac{{1+\sqrt{3}}}{4}$ | C. | $\frac{{\sqrt{3}-1}}{4}$i | D. | $\frac{{\sqrt{3}-1}}{4}$ |
分析 由z1求出$\overline{{z}_{1}}$,把$\overline{{z}_{1}}$,z2代入$\frac{\overline{{z}_{1}}}{{z}_{2}}$,然后利用复数代数形式的乘除运算化简,则答案可求.
解答 解:∵z1=1+i,z2=$\sqrt{3}$+i,
∴$\overline{{z}_{1}}=1-i$.
∴$\frac{\overline{{z}_{1}}}{{z}_{2}}$=$\frac{1-i}{\sqrt{3}+i}=\frac{(1-i)(\sqrt{3}-i)}{(\sqrt{3}+i)(\sqrt{3}-i)}=\frac{\sqrt{3}-1-(\sqrt{3}+1)i}{4}$=$\frac{\sqrt{3}-1}{4}-\frac{\sqrt{3}+1}{4}i$.
则$\frac{\overline{{z}_{1}}}{{z}_{2}}$的虚部为:$-\frac{1+\sqrt{3}}{4}$.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了共轭复数的求法,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
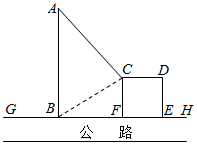 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°.
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,设AB=ykm,并在公路北侧建造边长为xkm的正方形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2} | B. | {x|x>-1} | C. | {x|x<-1} | D. | {x|x≤-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | [-1,1] | C. | {-1,-3,1,3} | D. | {-3,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
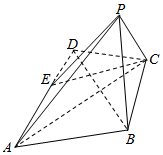 如图,在四边形ABCD中,AB=AD=4,BC=CD=$\sqrt{7}$,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PEC(点D与点P重合),使得平面PAC⊥平面ABCE,连接PA,PB.
如图,在四边形ABCD中,AB=AD=4,BC=CD=$\sqrt{7}$,点E为线段AD上的一点.现将△DCE沿线段EC翻折到PEC(点D与点P重合),使得平面PAC⊥平面ABCE,连接PA,PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com