
分析 命题p:方程$\frac{x^2}{m-4}+\frac{y^2}{2m-2}=1$表示焦点在y轴上的双曲线,则$\left\{\begin{array}{l}{2m-2>0}\\{m-4<0}\end{array}\right.$,解得;命题q:点(m,1)在椭圆$\frac{x^2}{8}+\frac{y^2}{2}=1$的内部,则$\frac{{m}^{2}}{8}$+$\frac{1}{2}$<1,解得m;命题r:函数f(m)=log2(m-a)的定义域为(a,+∞).
(1)若p∧q为真命题,则$\left\{\begin{array}{l}{1<m<4}\\{-2<m<2}\end{array}\right.$,解得m.
(2)p是r的充分不必要条件,可得a≤1.
解答 解:命题p:方程$\frac{x^2}{m-4}+\frac{y^2}{2m-2}=1$表示焦点在y轴上的双曲线,则$\left\{\begin{array}{l}{2m-2>0}\\{m-4<0}\end{array}\right.$,解得1<m<4;
命题q:点(m,1)在椭圆$\frac{x^2}{8}+\frac{y^2}{2}=1$的内部,则$\frac{{m}^{2}}{8}$+$\frac{1}{2}$<1,解得:-2<m<2;
命题r:函数f(m)=log2(m-a)的定义域为(a,+∞).
(1)若p∧q为真命题,则$\left\{\begin{array}{l}{1<m<4}\\{-2<m<2}\end{array}\right.$,解得1<m<2.
∴实数m的取值范围为(1,2).
(2)∵p是r的充分不必要条件,
∴∴a≤1.
∴实数a的取值范围是a≤1.
点评 本题考查了圆锥曲线的标准方程及其性质、函数的定义域、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
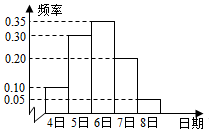 北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.
北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 6 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
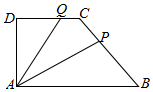 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com