
分析 求出直线l过定点(2,3),即函数y=loga(x+b)的图象定点(2,3),得出a3=2+b,求出b的取值范围,再求出a3-b2的最大值.
解答 解:直线l:(m+3n)x+2(m-n)y-8m=0可化为:
m(x+2y-8)+n(3x-2y)=0,
即$\left\{\begin{array}{l}{x+2y-8=0}\\{3x-2y=0}\end{array}\right.$,
解得x=2,y=3,
∴直线l过定点(2,3);
又直线l与函数y=loga(x+b)的图象恒有公共点,
即过定点(2,3),
∴loga(2+b)=3,
∴a3=2+b>1,即b>-1;
∴a3-b2=2+b-b2=-${(b-\frac{1}{2})}^{2}$+$\frac{9}{4}$≥$\frac{9}{4}$,
即a3-b2的最大值为$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了直线过定点的应用问题,也考查了对数函数与二次函数的图象与性质的应用问题,是综合性题目.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
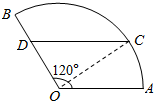 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )| A. | $50\sqrt{5}$ | B. | $50\sqrt{7}$ | C. | $50\sqrt{11}$ | D. | $50\sqrt{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -2i | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com