
分析 (1)an+1-an=2,${b_2}=-2{b_1},{b_{n+2}}=2{b_{n+1}},n∈{N^*}$,判断得出调查网,等比数列即可求解通项公式.
(2)①根据题目条件判断:数列{an}必为1,3,5,7,9,7,9,11,…,即前5项为首项为1,公差为2的等差数列,从第6项开始为首项7,公差为2的等差数列,
求解Sn即可.
②运用数列{bn}为“梦数列”且b1=-1,综合判断数列{bn}中有且只有两个负项.
假设存在正整数m,使得Sm+1=Tm,显然m≠1,且Tm为奇数,而{an}中各项均为奇数,即可得出;m必为偶数. 再运用不等式证明m≤6,求出数列即可.
解答 解:(1)数列{an},{bn}都为递增数列,
∴an+1-an=2,${b_2}=-2{b_1},{b_{n+2}}=2{b_{n+1}},n∈{N^*}$,
∴an=2n-1,${b_n}=\left\{\begin{array}{l}-1,n=1\\{2^{n-1}},n≥2\end{array}\right.$;
(2)①∵数列{an}满足:存在唯一的正整数r=5,使得ar+1<ar,且|an+1-an|=2,
∴数列{an}必为1,3,5,7,9,7,9,11,…,即前5项为首项为1,公差为2的等差数列,从第6项开始为首项7,公差为2的等差数列,
故${S_n}=\left\{\begin{array}{l}{n^2},n≤5\\{n^2}-4n+20,n≥6\end{array}\right.$;
②∵$b_{n+1}^2=4{b_n}^2$即bn+1=±2bn,
∴$|{b_n}|={2^{n-1}}$,
而数列{bn}为“梦数列”且b1=-1,
∴数列{bn}中有且只有两个负项.
假设存在正整数m,使得Sm+1=Tm,显然m≠1,且Tm为奇数,而{an}中各项均为奇数,
∴m必为偶数.
首先证明:m≤6.
若m>7,数列{an}中${({{S_{m+1}}})_{max}}=1+3+…+({2m+1})={(m+1)^2}$,
而数列{bn}中,bm必然为正,否则${T_m}=-1+{b_2}+…+({-{2^{m-1}}})≤-1+{2^1}+…+{2^{m-2}}+({-{2^{m-1}}})=-3<0$,显然矛盾;(※)
∴${({T_m})_{min}}=-1+{2^1}+…+({+{2^{m-3}}})+({-{2^{m-2}}})+{2^{m-1}}={2^{m-1}}-3$,
设${c_m}={2^{m-1}}-{(m+1)^2}-3$,
易得${d_m}={c_{m+1}}-{c_m}={2^{m-1}}-2m-3$,
而${d_{m+1}}-{d_m}={2^{m-1}}-2>0$,(m>7),
∴{dm}(m>7)为增数列,且d7>0进而{cm}(m>7)为增数列,而c8>0,
∴(Tm)min>(Sm)max,
即m≤6.
当m=6时,构造:{an}为1,3,1,3,5,7,9,…,{bn}为-1,2,4,8,-16,32,64,…
此时r1=2,r2=4
所以mmax=6,对应的r1=2,r2=4.
点评 本题综合考查了学生运用新定义,求解数列的问题,结合不等式,函数的思想求解,考查了分析问题,解决问题的能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{14}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{3}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\sqrt{13}$ | D. | $\frac{{1+\sqrt{13}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin4x | B. | cos4x | C. | sinx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
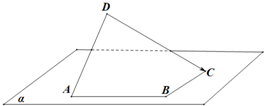
| A. | 2 | B. | 3 | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
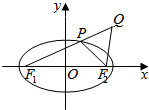 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com