
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
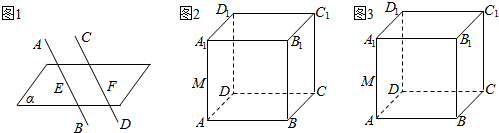
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(A+B)+sinC | B. | cos(A+B)-cosA | C. | sin2$\frac{A+B}{2}$+sin2$\frac{C}{2}$ | D. | sin$\frac{A+B}{2}$sin$\frac{C}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD是菱形.过AB的平面与侧棱CC1,DD1分别交于点E,F.
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD是菱形.过AB的平面与侧棱CC1,DD1分别交于点E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com