
���� ��1��bn=an+1-an=$\frac{{a}_{n}+{a}_{n+1}}{2}$-an+1=$\frac{{a}_{n}+{a}_{n+1}}{2}$=-$\frac{1}{2}$bn��b1=1�����õȱ����е�ͨ�ʽ�ɵ�bn����
��2���ɣ�1��֪��an+1-an=��-$\frac{1}{2}$��n-1�����á��ۼ���͡�������ȱ����е����ʽ�ɵ�an�����������еĵ����Լ��ɵó���
��3��${c_n}=\frac{3}{2}|{{a_n}-\frac{5}{3}}|$=��$\frac{1}{2}$��n-1���ɵ�Tn�T2-$��\frac{1}{2}��^{n-1}$�����$\frac{{T}_{n+1}-m}{{T}_{n}-m}$��cm+2����$\frac{2-��\frac{1}{2}��^{n}-m}{2-��\frac{1}{2}��^{n-1}-m}$��$��\frac{1}{2}��^{m+1}$����m��n�������ۼ��ɵó���
��� �⣺��1��bn=an+1-an=$\frac{{a}_{n}+{a}_{n+1}}{2}$-an+1=$\frac{{a}_{n}+{a}_{n+1}}{2}$=-$\frac{1}{2}$bn��b1=1
��{bn}�ù���Ϊ-$\frac{1}{2}$������Ϊ1�ĵȱ����У�{bn}��ͨ�ʽ��bn=��-$\frac{1}{2}$��n-1��
��2���ɣ�1��֪��an+1-an=��-$\frac{1}{2}$��n-1��
��n��1ʱ��an=a1+��a2-a1��+��a3-a2��+��+��an-an-1��
=1+1+��-$\frac{1}{2}$��+��-$\frac{1}{2}$��2+��+��-$\frac{1}{2}$��n-2
=$\frac{5}{3}$-$\frac{2}{3}$•��-$\frac{1}{2}$��n-1��
��a1=1=$\frac{5}{3}$-$\frac{2}{3}$��
������{an}��ͨ�ʽ��an=$\frac{5}{3}$-$\frac{2}{3}$•��-$\frac{1}{2}$��n-1��
��|an-$\frac{5}{3}$|=$\frac{1}{3}$•��$\frac{1}{2}$��n-2��
��|an-$\frac{5}{3}$|��$\frac{2}{9n}$�ȼ���3n•��$\frac{1}{2}$��n-1��1
��Dn=3n•��$\frac{1}{2}$��n-1��
��$\frac{{D}_{n+1}}{{D}_{n}}$=$\frac{n+1}{2n}$��
��D1=D2��n��1ʱ��Dn��Dn+1��
����ɵ�D4��1��D5��1��
������С������N��ֵ��4��
��3��${c_n}=\frac{3}{2}|{{a_n}-\frac{5}{3}}|$=��$\frac{1}{2}$��n-1��
��Tn�T$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=2-$��\frac{1}{2}��^{n-1}$��
��$\frac{{T}_{n+1}-m}{{T}_{n}-m}$��cm+2��
��$\frac{2-��\frac{1}{2}��^{n}-m}{2-��\frac{1}{2}��^{n-1}-m}$��$��\frac{1}{2}��^{m+1}$��
��m=1ʱ���ɵã�$\frac{1-��\frac{1}{2}��^{n}}{1-��\frac{1}{2}��^{n-1}}$��$\frac{1}{4}$����$3����\frac{1}{2}��^{n-1}$��n��1�����n��2ʱ�������
��m=2ʱ������ʽ��Ϊ��$\frac{1}{2}��$$\frac{1}{8}$��n��N*ʱ���������
��m��3ʱ����Ϊ��$\frac{m-2+��\frac{1}{2}��^{n}}{m-2+��\frac{1}{2}��^{n-1}}$��$��\frac{1}{2}��^{m+1}$������?n��N*�������
���� ���⿼���˵ȱ����е�ͨ�ʽ�����ʽ�����е��ƹ�ϵ�����еĵ����ԡ�����ʽ�Ľⷨ�����ʣ���������������������������������⣮


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m?����n?������m��n������ֱ�ߣ���ôn����ཻ | |
| B�� | �����ɦ�=m��n��m����n?����n?�£���n�Φ���n�Φ� | |
| C�� | ��m?����n?������m�֣�n�֣������ | |
| D�� | ��m�Φ���n�Φ£��Ҧ��Φ£���m��n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
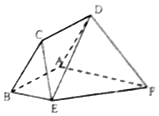 ��ͼ����֪����ABCD��ֱ������ABEF���ڵ�ƽ�滥�ഹֱ������BE��AF��AB��AF��AB=BE=$\frac{1}{2}$AF=2����CBA=$\frac{��}{3}$��
��ͼ����֪����ABCD��ֱ������ABEF���ڵ�ƽ�滥�ഹֱ������BE��AF��AB��AF��AB=BE=$\frac{1}{2}$AF=2����CBA=$\frac{��}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -$\frac{1}{2}$ | C�� | $\frac{1}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
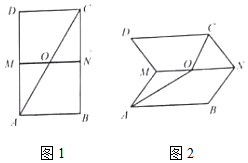 ��ͼ1��2����֪ABCD�Ǿ��Σ�M��N�ֱ�Ϊ��AD��BC���е㣬MN��AC���ڵ�O����MN������MNCD������AB=2��BC=4�������B-MN-C�Ĵ�СΪ�ȣ�
��ͼ1��2����֪ABCD�Ǿ��Σ�M��N�ֱ�Ϊ��AD��BC���е㣬MN��AC���ڵ�O����MN������MNCD������AB=2��BC=4�������B-MN-C�Ĵ�СΪ�ȣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com