
已知 中,顶点
中,顶点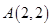 ,边
,边 上的中线
上的中线 所在直线的方程是
所在直线的方程是 ,边
,边 上高
上高 所在直线的方程是
所在直线的方程是 .
.
(1)求点 、C的坐标; (2)求
、C的坐标; (2)求 的外接圆的方程.
的外接圆的方程.
(1)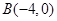
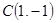 (2)
(2)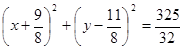 或
或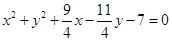
解析试题分析:(1)求 ,
,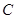 点就设
点就设 ,
,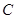 点的坐标,同时可以表示出
点的坐标,同时可以表示出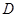 的坐标,根据
的坐标,根据 在
在 上,且
上,且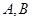 中点
中点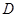 在
在 上.两式联立可求出
上.两式联立可求出 ;根据
;根据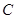 在
在 上,且
上,且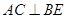 得到
得到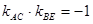 ,两式联立可求出
,两式联立可求出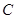 .
.
(2)所求的圆经过三角形的三个顶点,所以设出圆的一般方程,将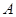 ,
, ,
,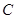 代入解方程组即可得到所求圆的方程.或者根据三角形的外接圆的圆心是各边垂直平分线的交点,所以可以根据(1)中的
代入解方程组即可得到所求圆的方程.或者根据三角形的外接圆的圆心是各边垂直平分线的交点,所以可以根据(1)中的 ,
,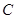 和已知的
和已知的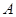 求两个边的垂直平分线,取其交点做圆心,该点到各个顶点的距离为半径,求出圆的方程.
求两个边的垂直平分线,取其交点做圆心,该点到各个顶点的距离为半径,求出圆的方程.
试题解析:(1)由题意可设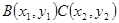 ,则
,则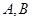 的中点
的中点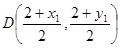 .
.
因为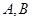 的中点
的中点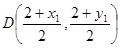 必在直线
必在直线 上,代入有
上,代入有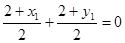 ①
①
又因为 在直线
在直线 上,所以代入有
上,所以代入有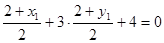 ②
②
由①②联立解得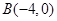 .则
.则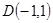 ,
,
因为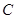 在直线
在直线 上,代入有
上,代入有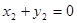 ③
③
又因为直线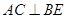 ,所以有
,所以有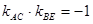 ,则有
,则有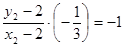 ④
④
根据③④有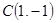 .
.
(2)因为三角形外接圆的圆心是各边垂直平分线的交点,
所以找到三角形两边的垂直平分线求得的交点就是外接圆的圆心,该点到各顶点的距离就是半径.
根据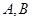 两点,可得斜率为
两点,可得斜率为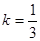 ,所以中垂线斜率为
,所以中垂线斜率为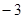 ,
,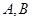 中点为
中点为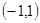 ,则中垂线为
,则中垂线为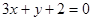 ⑤
⑤
同理可得直线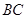 的中垂线为
的中垂线为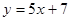 ⑥,
⑥,
由⑤⑥可得圆心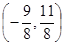 ,半径为
,半径为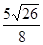 ,所以外接圆为
,所以外接圆为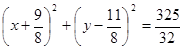
法二:(2)设 外接圆的方程为
外接圆的方程为 ,其中
,其中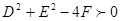 。
。
因为三角形的个顶点都在圆上,所以根据(1),将三点坐标代入有: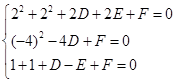 解得
解得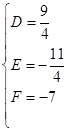
∴ 外接圆的方程为
外接圆的方程为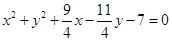 .
.
考点:三角形中,中线,垂线与各边,各个顶点的关系;外接圆的求法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(满分16分)如图:为保护河上古桥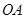 ,规划建一座新桥
,规划建一座新桥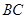 ,同时设立一个圆形保护区,规划要求,新桥
,同时设立一个圆形保护区,规划要求,新桥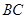 与河岸
与河岸 垂直;保护区的边界为圆心
垂直;保护区的边界为圆心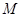 在线段
在线段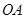 上并与
上并与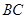 相切的圆,且古桥两端
相切的圆,且古桥两端 和
和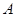 到该圆上任一点的距离均不少于80
到该圆上任一点的距离均不少于80 ,经测量,点
,经测量,点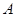 位于点
位于点 正北方向60
正北方向60 处,点
处,点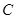 位于点
位于点 正东方向170
正东方向170 处,(
处,(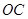 为河岸),
为河岸),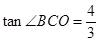 .
.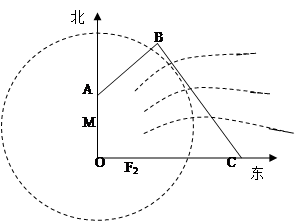
(1)求新桥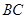 的长;
的长;
(2)当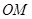 多长时,圆形保护区的面积最大?
多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆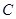 :
: (
(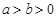 )过点(2,0),且椭圆C的离心率为
)过点(2,0),且椭圆C的离心率为 .
.
(1)求椭圆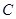 的方程;
的方程;
(2)若动点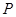 在直线
在直线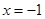 上,过
上,过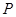 作直线交椭圆
作直线交椭圆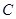 于
于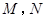 两点,且
两点,且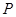 为线段
为线段 中点,再过
中点,再过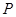 作直线
作直线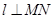 .求直线
.求直线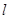 是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.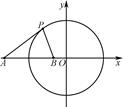
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有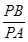 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直角坐标系中,射线OA: x-y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.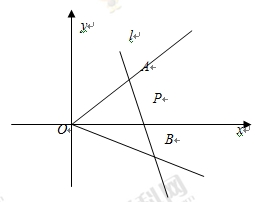
(1)当AB中点为P时,求直线AB的斜率
(2)当AB中点在直线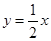 上时,求直线AB的方程.
上时,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com