
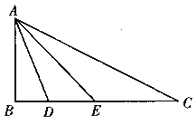
 如图,在△ABC中,∠B=90°,∠BAD=∠DAE=∠EAC,BD=2,DE=3.
如图,在△ABC中,∠B=90°,∠BAD=∠DAE=∠EAC,BD=2,DE=3.分析 (Ⅰ)根据tanθ=$\frac{BD}{AB}$,tan2θ=$\frac{BE}{AB}$,利用正切函数的二倍角公式,即可求得tanθ,即可求得AB的长;
(Ⅱ)sinC=sin($\frac{π}{2}$-∠BAC)cos∠BAC=cos(θ+2θ),利用二倍角公式即可求得sinC..
解答 解:(Ⅰ)设∠BAD=θ<90°,在Rt△ABD中,tanθ=$\frac{BD}{AB}$,AB=$\frac{BD}{tanθ}$,
在Rt△ABE中,tan2θ=$\frac{BE}{AB}$,AB=$\frac{BE}{tan2θ}$,
∴$\frac{BD}{tanθ}$=$\frac{BE}{tan2θ}$,则5tanθ=2tan2θ,
即5tanθ=$\frac{2×2tanθ}{1-ta{n}^{2}θ}$,即5tan2θ=1,解得$tanθ=\frac{{\sqrt{5}}}{5}$(负值舍去),
因此$AB=\frac{2}{tanθ}=2\sqrt{5}$.
(Ⅱ)由题意知0°<θ<2θ<3θ<90°.
因为$tanθ=\frac{{\sqrt{5}}}{5}$,则$sinθ=\frac{{\sqrt{6}}}{6}$,$cosθ=\frac{{\sqrt{30}}}{6}$,
则sin2θ=2sinθcosθ=$\frac{\sqrt{5}}{3}$,cos2θ=cos2θ-cos2θ=$\frac{2}{3}$,即$sin2θ=\frac{{\sqrt{5}}}{3}$,$cos2θ=\frac{2}{3}$.
sinC=sin($\frac{π}{2}$-∠BAC)cos∠BAC=cos(θ+2θ)=cosθcos2θ-sinθsin2θ,=$\frac{\sqrt{30}}{6}$×$\frac{2}{3}$-$\frac{\sqrt{6}}{6}$×$\frac{\sqrt{5}}{3}$=$\frac{\sqrt{30}}{18}$
∴sinC=$\frac{\sqrt{30}}{18}$.
点评 本题考查同角三角函数的基本关系,诱导公式,二倍角公式,两角和的余弦公式,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=lnx | C. | y=$\frac{1}{\sqrt{x}}$ | D. | y=10x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
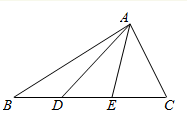 如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.
如图,D、E分别是△ABC的三等分点,设$\overrightarrow{AD}$=$\overrightarrow{m}$,$\overrightarrow{AE}$=$\overrightarrow{n}$,∠BAC=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 25 | C. | 27 | D. | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com