练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若x∈(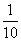，1)，a＝lgx，b＝lg2x，c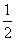＝lgx，则a、b、c的大小关系是(　　)

    A．a<b<c                                                      B．a<c<b

    C．c<a<b                                                      D．b<c<a


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    函数y＝f(x)的定义域为[－2,0)∪(0,2]，其图象上任一点P(x，y)满足＋y2＝1，若函数y＝f(x)的值域是(－1,1)，则f(x)一定是(　　)

    A．奇函数                                                    B．偶函数

    C．单调函数                                                 D．幂函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝loga(2x＋b－1)(a>0，a≠1)的图象如图所示，则a，b满足的关系是(　　)

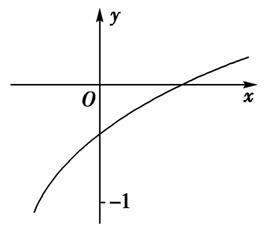
    A．0<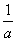<b<1

    B．0<b<<1

    C．0<<a<1

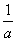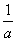    D．0<<<1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝ax(a>0且a≠1)在[1,2]上的最大值比最小值大，则a的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某工厂某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C(x)，当年产量不

    足80千件时，C(x)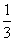＝x2＋10x(万元)；当年产量不小于80千件时，C(x)＝51x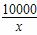＋－1450(万元)．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．

    (1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式；

    (2)年产量为多少千件时，该厂在这种商品的生产中所获利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a>b>1，c<0，给出下列三个结论：

    ①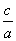>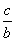；  ②ac<bc；

    ③logb(a－c)>loga(b－c)．

    其中所有的正确结论的序号是(　　)

    A．①                                                           B．①②

    C．②③                                                        D．①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝loga(ax－1)(a>0且a≠1)．

    (1)证明函数f(x)的图象在y轴的一侧；

    (2)设A(x1，y1)、B(x2，y2)(x1<x2)是f(x)图象上两点，证明直线AB的斜率大于0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)＝lg(＋a)是奇函数，且在x＝0处有意义，则该函数是(　　)

    A．(－∞，＋∞)上的减函数

    B．(－∞，＋∞)上的增函数

    C．(－1,1)上的减函数

    D．(－1,1)上的增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义域为R的函数f(x)为奇函数，且满足f(x＋2)＝－f(x)，当x∈[0,1]时，f(x)＝2x－1.

    (1)求f(x)在[－1,0)上的解析式；

    (2)求f(log24)的值．

    查看答案和解析>>

    同步练习册答案