
| A. | 100钱 | B. | 101钱 | C. | 107钱 | D. | 108钱 |
分析 设公差为d,七人的钱依次为a-3d,a-2d,a-d,a,a+d,a+2d,a+3d,由题意可得$\left\{\begin{array}{l}{2a-5d=237}\\{3a+6d=261}\end{array}\right.$,解得即可.
解答 解:因为七人的钱数为等差数列,
设公差为d,七人的钱依次为a-3d,a-2d,a-d,a,a+d,a+2d,a+3d,
由题意可得$\left\{\begin{array}{l}{2a-5d=237}\\{3a+6d=261}\end{array}\right.$,
解得a=101,d=-7,
所以丙的钱数为101+7=108,
故选:D
点评 本题考查等差数列的通项公式,考查学生利用数学知识解决实际问题,是基础的计算题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>c>a | C. | b>a>c | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
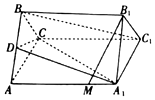 如图,在正三棱柱ABC-A1B1C1中,点D是AB的上一点,且AD=tAB.
如图,在正三棱柱ABC-A1B1C1中,点D是AB的上一点,且AD=tAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|1≤x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com