
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
分析 利用复数代数形式的乘除运算化简,再由实部大于0且虚部小于0联立求得实数a的取值范围.
解答 解:∵$z=\frac{{a+2{i^3}}}{2-i}$=$\frac{a-2i}{2-i}=\frac{(a-2i)(2+i)}{(2-i)(2+i)}=\frac{2a+2+(a-4)i}{5}$在复平面内对应的点在第四象限,
∴$\left\{\begin{array}{l}{2a+2>0}\\{a-4<0}\end{array}\right.$,解得-1<a<4.
∴实数a的取值范围是(-1,4).
故选:C.
点评 本题考查复数代数式的乘除运算,考查复数的代数表示法及其几何意义,是基础的计算题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
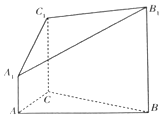 如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1
如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
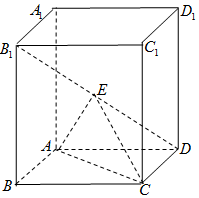 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | 1 | C. | 2 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{e})$ | B. | $(0,\frac{1}{2e})$ | C. | $[\frac{ln3}{3},\frac{1}{e})$ | D. | $[\frac{ln3}{3},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100钱 | B. | 101钱 | C. | 107钱 | D. | 108钱 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com