
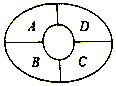
 如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为260.
如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为260. 分析 根据题意,分3步进行分析:①、先分析A区域,可以在5种颜色中选1种,②、对于B区域,需要在剩下的4种颜色种任选1种,③、对于C、D区域,分“D区域与B区域同色”和“D区域与B区域不同色”两种情况讨论即可,由分步计数原理计算可得答案.
解答 解:根据题意,分3步进行分析:
①、对于A区域,可以在5种颜色中选1种,即有5种情况,
②、对于B区域,需要在剩下的4种颜色种任选1种,即有4种情况,
③、对于C、D区域,
若D区域与B区域同色,C区域可以在剩下的4种颜色种任选1种,即有4种情况,
若D区域与B区域不同色,则D区域需要在除A、B的颜色外的3种颜色种任选1种,即有3种情况,
C区域可以在除B、D的颜色外的3种颜色种任选1种,即有3种情况,
则C、D区域有4+3×3=13种情况;
则不同的安排方法种数5×4×13=260种;
故答案为:260.
点评 本题考查排列、组合的应用,关键是根据题意,如何分步分析和分类讨论.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 60° | C. | 120° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com