练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．高二（7）班参加冬令营的6位同学排成一排照相，甲乙必须相邻且甲、乙、丙必须从左到右的排法种数为（　　）
    A．120B．60C．36D．72

    分析 根据题意，假设剩余的3人是A、B、C，先将甲、乙、丙排好，分析空位的数目，依次分析A、B、C的安排方法数目，由分步计数原理计算可得答案．

    解答 解：根据题意，假设剩余的3人是A、B、C，
    先将甲、乙、丙从左到右排好，排好后，除去甲乙之间的空位有3个空位，
    在3个空位中任选一个，安排A，有C31=3种情况，排好后，除去甲乙之间的空位有4个空位，
    在4个空位中任选一个，安排B，有C41=4种情况，排好后，除去甲乙之间的空位有5个空位，
    在5个空位中任选一个，安排C，有C51=5种情况，
    则一共有3×4×5=60种安排方法；
    故选：B．

    点评 本题考查排列、组合的应用，注意“甲、乙、丙必须从左到右”排列这一条件，用插空法分析．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

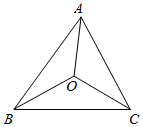    20．如图，已知O为△ABC的外心，角A、B、C的对边分别为a、b、c．
    （1）若5$\overrightarrow{OA}$+4$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$，求cos∠BOC的值；
    （2）若$\overrightarrow{CO}$•$\overrightarrow{AB}$=$\overrightarrow{BO}$•$\overrightarrow{CA}$，求$\frac{{b}^{2}+{c}^{2}}{{a}^{2}}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．对于椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$，下面说法正确的是（　　）
    A．长轴长为2B．短轴长为3C．离心率为$\frac{1}{2}$D．焦距为1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．在△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinb，且$B＞\frac{π}{2}$，则sinA+sinC的最大值是$\frac{9}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．等差数列{an}的前n项和为Sn，若S2=2，S4=8，则S6等于18．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

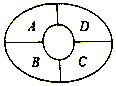    15．如图某综艺节目现场设有A，B，C，D四个观众席，现有由5不同颜色的马甲可供现场观众选择，同一观众席上的马甲的颜色相同，相邻观众席上的马甲的颜色不相同，则不同的安排方法种数为260．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

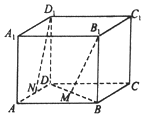    2．如图所示，在正方体ABCD-A1B1C1D1中，己知棱长为a，M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为（　　）
    A．-$\frac{\sqrt{15}}{15}$B．$\frac{\sqrt{30}}{10}$C．-$\frac{\sqrt{30}}{10}$D．$\frac{\sqrt{15}}{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知f（x）=lnx+$\frac{1}{8}$x2．
    （1）求曲线f（x）在x=1处的切线方程；
    （2）设P为曲线f（x）上的点，求曲线C在点P处切线的斜率的最小值及倾斜角α的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

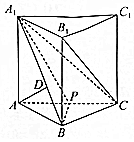    20．如图，直三棱柱ABC-A1B1C1中，AD⊥平面A1BC，其垂足D落在直线A1B上，P为AC的中点．
    （Ⅰ）求证：B1C∥平面A1PB；
    （Ⅱ）若AD=$\sqrt{3}$，AB=BC=2，求直线A1C与平面AA1B1B所成的角的正切值．

    查看答案和解析>>

    同步练习册答案