
| A. | (0,1) | B. | (-1,0) | C. | (1,+∞) | D. | (-∞,-1) |
分析 先利用向量数量积运算性质,将$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,两边平方,消去半径得m、n的数量关系,利用向量加法的平行四边形法则,可判断m+n一定为负值,从而可得正确结果.
解答 解:∵|OC|=|OB|=|OA|,$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$,
∴1=m2+n2+2mncos∠AOB
当∠AOB=60°时,m2+n2+mn=1,m<0,n>0,即(m+n)2-mn=1,即(m+n)2=1+mn<1,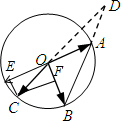
所以(m+n)2<1,
∴-1<m+n<1,当$\overrightarrow{OA}$,$\overrightarrow{OB}$趋近射线OD,
由平行四边形法则$\overrightarrow{OC}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,此时显然m<0,n>0,且|m|>|n|,
∴m+n<0,所以m+n的取值范围(-1,0).
故选B.
点评 本题主要考查了平面向量的几何意义,平面向量加法的平行四边形法则,平面向量基本定理,平面向量数量积运算的综合运用,属于中档题.


科目:高中数学 来源: 题型:填空题
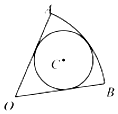 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
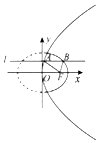 如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )
如图动直线l:y=b与抛物线y2=4x交于点A,与椭圆$\frac{x^2}{2}+{y^2}=1$交于抛物线右侧的点B,F为抛物线的焦点,则AF+BF+AB的最大值为( )| A. | 3 | B. | $3\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | 2 | C. | $\frac{{\sqrt{5}+1}}{2}$或2 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com