在
中，已知
，
且
.
（1）求角
和
的值；
（2）若的边
，求边
的长.
阅读快车系列答案科目：高中数学 来源： 题型：解答题
（12分）（2011•湖北）设△ABC的内角A、B、C所对的边分别为a、b、c，已知a=1，b=2，cosC=
（Ⅰ）求△ABC的周长；
（Ⅱ）求cos（A﹣C）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，
、
是两个小区所在地，、到一条公路
的垂直距离分别为
，
，两端之间的距离为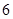
.
（1）某移动公司将在之间找一点
，在处建造一个信号塔，使得对
、的张角与对
、的张角相等，试确定点的位置.
（2）环保部门将在之间找一点
，在
处建造一个垃圾处理厂，使得对、所张角最大，试确定点的位置.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度.
(2)求sinα的值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
己知A、B、C分别为△ABC的三边a、b、c所对的角，向量
，且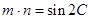
.
（1）求角C的大小：
（2）若sinA，sinC，sinB成等差数列，且
，求边c的长．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
风景秀美的湖畔有四棵高大的银杏树，记做
、
、
、
，欲测量、两棵树和、两棵树之间的距离，但湖岸部分地方围有铁丝网不能靠近，现在可以方便的测得、两点间的距离为
米，如图，同时也能测量出
，
，
，
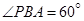，则、两棵树和、两棵树之间的距离各为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在△ABC中，内角A，B，C的对边分别为a，b，c．已知cosA＝
，sinB＝
cosC．
(1)求tanC的值；
(2)若a＝
，求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
；（2）
.
并结合两角差的余弦公式求出
，然后再结合
，最后再利用两角和的正弦公式求出
，
，得
且
， 
，
，
，
，
，
在
，
；
，
.
，函数
．
的对称中心； 
中，
分别是角
对边，且
，且
，求
的取值范围．
， 