
【题目】在三棱柱ABOA′B′O′中,∠AOB=90°,侧棱OO′⊥面OAB,OA=OB=OO′=2.若C为线段O′A的中点,在线段BB′上求一点E,使|EC|最小.
【答案】当z=1时,|EC|取得最小值为![]() ,此时E(0,2,1)为线段BB′的中点
,此时E(0,2,1)为线段BB′的中点
【解析】试题分析:先根据条件建立空间直角坐标系,设立各点坐标,则根据两点间距离公式得|EC|,最后根据二次函数最值求法得最小值
试题解析:解

如图所示,
以三棱原点,以OA、OB、OO′所在直线分别为x轴、y轴、z轴建立空间直角坐标系Oxyz.
由OA=OB=OO′=2,得A(2,0,0)、B(0,2,0)、O(0,0,0),A′(2,0,2)、B′(0,2,2)、O′(0,0,2).
由C为线段O′A的中点得C点坐标为(1,0,1),设E点坐标为(0,2,z),
∴|EC|=![]()
=![]() .
.
故当z=1时,|EC|取得最小值为![]() .
.
此时E(0,2,1)为线段BB′的中点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() 上的任意一点,点
上的任意一点,点![]() 为圆
为圆![]() 的圆心,点
的圆心,点![]() 与点
与点![]() 关于平面直角系的坐标原点对称,线段
关于平面直角系的坐标原点对称,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 交于点
交于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若轨迹![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,求
两点,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①在函数![]() 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为![]() ;②函数
;②函数![]() 的图象关于点
的图象关于点![]() 对称;③“
对称;③“ ![]() 且
且![]() ”是“
”是“![]() ”的必要不充分条件;④已知命题
”的必要不充分条件;④已知命题![]() :对任意的
:对任意的![]() ,都有
,都有![]() ,则
,则![]() 是:存在
是:存在![]() ,使得
,使得![]() ;⑤在
;⑤在![]() 中,若
中,若![]() ,
, ![]() ,则角
,则角![]() 等于
等于![]() 或
或![]() .其中所有真命题的个数是__________.
.其中所有真命题的个数是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线l:(m+3)x-(m+2)y+m=0与圆C:(x-3)2+(y-4)2=9.
(1)求证:无论m为何值,直线l总过定点A,并说明直线l与圆C总相交.
(2)m为何值时,直线l被圆C所截得的弦长最小?请求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.35
B.﹣3
C.3
D.﹣0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国
微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国![]() 标准采用世卫组织设定的最宽限值.即
标准采用世卫组织设定的最宽限值.即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
某市环保局从360天的市区![]() 监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 32 | 28 | 25 | 31 | 34 | 33 | 45 | 44 | 63 | 68 |
(1)从5月到10月的这6个数据中任取2个数值,求这个2个数值均为二级的概率;
(2)求月均值![]() 关于月份
关于月份![]() 的回归直线方程
的回归直线方程![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
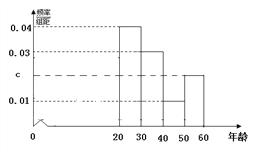
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com