
分析 利用等差数列的通项公式及其前n项和公式即可得出.
解答 解:设等差数列{an}的公差为d,∵a1+a3=8,且a42=a2a9,
∴$\left\{\begin{array}{l}{2{a}_{1}+2d=8}\\{({a}_{1}+3d)^{2}=({a}_{1}+d)({a}_{1}+8d)}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=4}\\{d=0}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=3}\end{array}\right.$.
∴当$\left\{\begin{array}{l}{{a}_{1}=4}\\{d=0}\end{array}\right.$时,an=4,Sn=4n.
当$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=3}\end{array}\right.$时,an=1+3(n-1)=3n-2,Sn=$\frac{n(1+3n-2)}{2}$=$\frac{3}{2}{n}^{2}$-$\frac{1}{2}$n.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| x | $-\frac{π}{4}$ | 0 | $\frac{π}{6}$ | $\frac{π}{4}$ | $\frac{π}{2}$ | $\frac{3π}{4}$ |
| f(x) | 0 | 1 | $\frac{1}{2}$ | 0 | -1 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是正方形,SA=SB=SC=SD,P是棱SC上的点,M,N分别是棱SB,SD上的点,SP:PC=1:2,SN:ND=2:1,SM:MB=2:1
如图,四边形ABCD是正方形,SA=SB=SC=SD,P是棱SC上的点,M,N分别是棱SB,SD上的点,SP:PC=1:2,SN:ND=2:1,SM:MB=2:1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
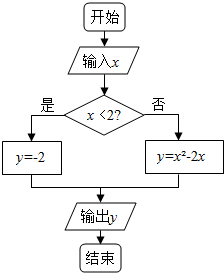 据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题
据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com