
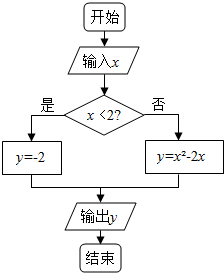
 据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题
据如图所示的程序框图,说明该流程图解决什么问题,写出相应的算法.并回答下列问题分析 根据程序框图可知求函教f(x)=$\left\{\begin{array}{l}{y={x}^{2}-2x,x≥2}\\{y=-2,x<2}\end{array}\right.$的函数值的问题,写出算法步骤即可,根据函数的表达式分别求出(1),(2),(3).
解答 解:程序框图解决的是求函教f(x)=$\left\{\begin{array}{l}{y={x}^{2}-2x,x≥2}\\{y=-2,x<2}\end{array}\right.$的函数值的问题,
算法步骤如下:
第一步:输入x
第二步:如果x<2,则使y=-2;
否则,y=x2-2x
第三步:输出y.
(1)输入的x值为5,
∴y=52-2×5=15,
(2):要使输出的函数值为8,则x2-2x=8,
∴x=4或x=-2(舍去)
故输入的值应为4;
(3):x≥2时,y=x2-2x=(x-1)2-1≥0,
x<2时,y=-2
又-2<0,
故要使输出的y值最小,只要输入的x满足x<2即可.
点评 本题考查了程序框图的问题,以及简单的算法步骤,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,3] | B. | [-1,3] | C. | [-3,3] | D. | [-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | [-$\sqrt{3}$,$\sqrt{3}$] | C. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com