
分析 (1)方法一,用综合法,即利用作差法;方法二,分析法,两边平方法;
(2)要证明当x>-1时,(1+x)m≥1+mx,我们要先证明m=1时,(1+x)m≥1+mx成立,再假设m=k时,(1+x)m≥1+mx成立,进而证明出m=k+1时,(1+x)m≥1+mx也成立,即可得到对于任意正整数m:当x>-1时,(1+x)m≥1+mx.
解答 (1)证明 方法一 用综合法
$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$-$\sqrt{a}$-$\sqrt{b}$=$\frac{a\sqrt{a}+b\sqrt{b}-a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}$
=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{\sqrt{ab}}$=$\frac{(\sqrt{a}-\sqrt{b})2(\sqrt{a}+\sqrt{b})}{\sqrt{ab}}$>0,
所以$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$.
方法二 用分析法
要证$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$,
只要证$\frac{a2}{b}$+$\frac{b2}{a}$+2$\sqrt{ab}$>a+b+2$\sqrt{ab}$,
即要证a3+b3>a2b+ab2,
只需证(a+b)(a2-ab+b2)>ab(a+b),
即需证a2-ab+b2>ab,
只需证(a-b)2>0,
因为a≠b,所以(a-b)2>0恒成立,
所以$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$>$\sqrt{a}$+$\sqrt{b}$成立.
(2)证明①当m=1时,原不等式成立;
当m=2时,左边=1+2x+x2,右边=1+2x,
因为x2≥0,所以左边≥右边,原不等式成立;
②假设当m=k(k≥1,k∈N*)时,不等式成立,
即(1+x)k≥1+kx,则当m=k+1时,
因为x>-1,所以1+x>0.
于是在不等式(1+x)k≥1+kx两边同时乘以1+x得
(1+x)k•(1+x)≥(1+kx)(1+x)=1+(k+1)x+kx2
≥1+(k+1)x.
所以(1+x)k+1≥1+(k+1)x,
即当m=k+1时,不等式也成立.
综合①②知,对一切正整数m,不等式都成立.
点评 本题考查了综合法和分析法以及数学归纳法证明不等式成立的问题,掌握这些方法的步骤是关键,属于中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
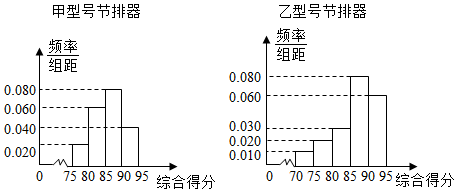
| 综合得分k的取值范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类型 | A类 | B类 | C类 |
| 已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
| 已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [10,25) | [25,40) | [40,55] |
| 成绩优秀 | 670 | a | b |
| 成绩一般 | 80 | 60 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com