Question

5．正三棱台的上、下底面的边长分别是3和6．
（1）若侧面与底面所成的角为60°，求此三棱台的体积；
（2）若侧棱与底面所成的角为60°，求此三棱台的侧面积．

Answer 1

分析 由题意画出图形，由已知求出上下底面面积．
（1）当侧面与底面所成的角为60°时，解三角形求出棱台的高，代入体积公式得答案；
（2）当侧棱与底面所成的角为60°时，解三角形求出棱台的斜高，代入侧面积公式得答案．

解答 解：如图，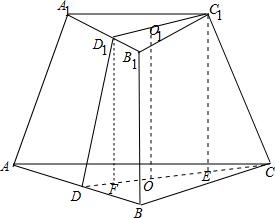

作C₁D₁⊥A₁B₁，CD⊥AB，作C₁E⊥CD=E，D₁F⊥CD=F，
∵上底面边长为3，∴上底面边A₁B₁上的高${C}_{1}{D}_{1}=\frac{3\sqrt{3}}{2}$，
则${O}_{1}{D}_{1}=\frac{\sqrt{3}}{2}，{O}_{1}{C}_{1}=\sqrt{3}$，
∵下底面边长为6，∴下底面边AB上的高为CD=$3\sqrt{3}$，
则$OD=\sqrt{3}，OC=2\sqrt{3}$，
∴$DF=OD-{O}_{1}{D}_{1}=\frac{\sqrt{3}}{2}$，$CE=OC-{O}_{1}{C}_{1}=\sqrt{3}$，
上底面面积为$\frac{1}{2}×3×\frac{3\sqrt{3}}{2}=\frac{9\sqrt{3}}{4}$，下底面面积为$\frac{1}{2}×6×3\sqrt{3}=9\sqrt{3}$．
（1）若正三棱台侧面与底面成60°，即∠D₁DF=60°，
∴三棱台的高为$\sqrt{3}DF=\frac{3}{2}$，
则三棱台体积V=$\frac{1}{3}×\frac{3}{2}（\frac{9\sqrt{3}}{4}+9\sqrt{3}+\sqrt{\frac{9\sqrt{3}}{4}×9\sqrt{3}}）$=$\frac{63\sqrt{3}}{8}$；
（2）若正三棱台侧棱与底面成60°，即∠C₁CE=60°，
∴三棱台的高为$\sqrt{3}CE=3$，
则三棱台的斜高为$\sqrt{{3}^{2}+（\frac{\sqrt{3}}{2}）^{2}}=\frac{\sqrt{39}}{2}$，
∴此三棱台的侧面积为3×$\frac{1}{2}×\frac{\sqrt{39}}{2}（3+6）=\frac{36\sqrt{39}}{4}$．

点评 本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是中档题．