
| A. | $\frac{3}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$ | B. | $\frac{1}{3}\overrightarrow{a}$+$\frac{2}{3}\overrightarrow{b}$ | C. | $\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$ | D. | $\frac{2}{3}\overrightarrow{a}$+$\frac{1}{3}\overrightarrow{b}$ |
分析 根据△DEF∽△BEA得对应边成比例,得到DF与FC之比,做FG平行BD交AC于点G,使用已知向量表示出要求的向量,即可得出结论.
解答 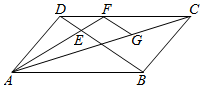 解:∵△DEF∽△BEA,
解:∵△DEF∽△BEA,
∴DF:BA═DE:BE=1:3;
作FG平行BD交AC于点G,
∴FG:DO=2:3,CG:CO=2:3,
∴$\stackrel{→}{GF}$=$\frac{1}{3}$$\stackrel{→}{b}$,
∵$\stackrel{→}{AG}$=$\stackrel{→}{AO}$+$\stackrel{→}{OG}$=$\frac{2}{3}$$\stackrel{→}{AC}$=$\frac{2}{3}$$\stackrel{→}{a}$,
∴$\stackrel{→}{AF}$=$\stackrel{→}{AG}$+$\stackrel{→}{GF}$=$\frac{2}{3}$$\stackrel{→}{a}$+$\frac{1}{3}$$\stackrel{→}{b}$,
故选:D.
点评 本题考查向量的线性运算及其几何意义,考查学生的计算能力,灵活运用题目的条件是解题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
 观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….
观察下列各个等式:12=1,12+22=5,12+22+32=14,12+22+32+42=30,….查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 使得$\sum_{i=1}^{n}$[yi-(ai+bxi)]最小 | B. | 使得$\sum_{i=1}^{n}$|yi-(ai+bxi)|最小 | ||
| C. | 使得$\sum_{i=1}^{n}$[yi2-(ai+bxi)2]最小 | D. | 使得$\sum_{i=1}^{n}$[yi-(ai+bxi)]2最小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
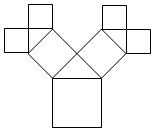 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com