
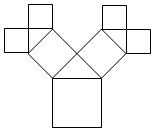
 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$. 分析 推导出正方形个数{an}是以首项为1,公比为2的等比数列,从而得到正方形个数为8,再推导出第一个正方形的边长{bn}是以$\frac{{\sqrt{2}}}{2}$为首项,公比为$\frac{{\sqrt{2}}}{2}$的等比数列,由此能求出最小的正方形的边长.
解答 解:设初始正方形个数为a1=1,依次得到a2=2,a3=4,
每一个正方形都可以得到2个正方形,
∴满足$\frac{{{a_{n+1}}}}{a_n}=2$,是以首项为1,公比为2的等比数列,
∴正方形个数的和为${s_n}=\frac{{1-{2^n}}}{1-2}=255$,解得n=8,
第一个正方形的边长设为${b_1}=\frac{{\sqrt{2}}}{2}$,然后满足$\frac{{{b_{n+1}}}}{b_n}=\frac{{\sqrt{2}}}{2}$,
∴数列{bn}是以$\frac{{\sqrt{2}}}{2}$为首项,公比为$\frac{{\sqrt{2}}}{2}$的等比数列,
∴${b_8}={b_1}•{q^{8-1}}=\frac{{\sqrt{2}}}{2}×{({\frac{{\sqrt{2}}}{2}})^7}={({\frac{{\sqrt{2}}}{2}})^8}=\frac{1}{16}$,
∴最小的正方形的边长为$\frac{1}{16}$.
故答案为:$\frac{1}{16}$.
点评 本题考查最小正方形的求法,是中档题,解题时要认真审题,注意等比数列、等差数列的性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}\overrightarrow{a}$+$\frac{1}{4}\overrightarrow{b}$ | B. | $\frac{1}{3}\overrightarrow{a}$+$\frac{2}{3}\overrightarrow{b}$ | C. | $\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$ | D. | $\frac{2}{3}\overrightarrow{a}$+$\frac{1}{3}\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $C_{10}^5$ | B. | $C_{10}^5•{3^5}•{({-2})^5}$ | C. | $C_{10}^4•{3^6}•{({-2})^4}$ | D. | $C_{10}^4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某媒体为了解某地区大学生晚上放学后使用手机上网情况,随机抽取了100名大学生进行调查.如图是根据调查结果绘制的学生每晚使用手机上网平均所用时间的频率分布直方图.将时间不低于40分钟的学生称为“手机迷”.
某媒体为了解某地区大学生晚上放学后使用手机上网情况,随机抽取了100名大学生进行调查.如图是根据调查结果绘制的学生每晚使用手机上网平均所用时间的频率分布直方图.将时间不低于40分钟的学生称为“手机迷”.| 非手机迷 | 手机迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | $(\frac{2}{3},+∞)$ | C. | $(-∞,0)∪(\frac{2}{3},+∞)$ | D. | $(0,\frac{2}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
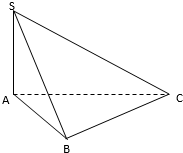 如图,在三棱锥S-ABC中,AC⊥BC,AC=3,BC=4,SA=SB=$\sqrt{13}$,平面SAB⊥平面ABC,则二面角S-BC-A的大小为( )
如图,在三棱锥S-ABC中,AC⊥BC,AC=3,BC=4,SA=SB=$\sqrt{13}$,平面SAB⊥平面ABC,则二面角S-BC-A的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}-1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com