
分析 根据定义求出tanα的值,再化简题目中的代数式并代入求值.
解答 解:角α终边上一点P(-4,3 ),
∴tanα=$\frac{y}{x}$=-$\frac{3}{4}$;
∴$\frac{cos(\frac{3π}{2}+α)sin(-5π-α)}{cos(6π-α)sin(\frac{π}{2}+α)tan(-3π+α)}$
=$\frac{sinα[-sin(4π+π+α)]}{cos(-α)cosαtanα}$
=$\frac{sinα[-sin(π+α)]}{cos(-α)cosα•\frac{sinα}{cosα}}$
=$\frac{sinαsinα}{cosαsinα}$=tanα=-$\frac{3}{4}$.
点评 本题考查了三角函数的定义、化简与求值问题,是基础题目.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 使得$\sum_{i=1}^{n}$[yi-(ai+bxi)]最小 | B. | 使得$\sum_{i=1}^{n}$|yi-(ai+bxi)|最小 | ||
| C. | 使得$\sum_{i=1}^{n}$[yi2-(ai+bxi)2]最小 | D. | 使得$\sum_{i=1}^{n}$[yi-(ai+bxi)]2最小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
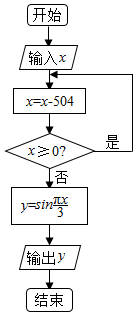
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
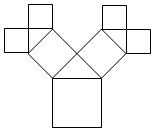 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com