
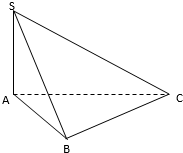
 如图,在三棱锥S-ABC中,AC⊥BC,AC=3,BC=4,SA=SB=$\sqrt{13}$,平面SAB⊥平面ABC,则二面角S-BC-A的大小为( )
如图,在三棱锥S-ABC中,AC⊥BC,AC=3,BC=4,SA=SB=$\sqrt{13}$,平面SAB⊥平面ABC,则二面角S-BC-A的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 取AB中点D,BC中点E,连结SD、SE、DE,由已知条件推导出∠SED是二面角S-BC-A的平面角,由此能求出二面角S-BC-A的大小.
解答 解:取AB中点D,BC中点E,连结SD、SE、DE,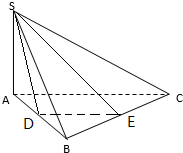 ∵在三棱锥S-ABC中,AC⊥BC,AC=3,BC=4,SA=SB=$\sqrt{13}$,平面SAB⊥平面ABC,
∵在三棱锥S-ABC中,AC⊥BC,AC=3,BC=4,SA=SB=$\sqrt{13}$,平面SAB⊥平面ABC,
∴SD⊥平面ABC,DE⊥BC,∴SE⊥BC,
∴∠SED是二面角S-BC-A的平面角,
且SD=$\sqrt{13-\frac{25}{4}}$=$\frac{3\sqrt{3}}{2}$,DE=$\frac{1}{2}AC$=$\frac{3}{2}$,SD⊥DE,
∴tan∠SED=$\frac{SD}{DE}$=$\frac{\frac{3\sqrt{3}}{2}}{\frac{3}{2}}$=$\sqrt{3}$.
∴∠SED=60°.
∴二面角S-BC-A的大小为60°.
故选:C
点评 本题考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
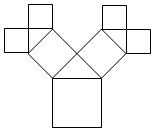 如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.
如图所示是毕达哥拉斯(Pythagoras)的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,若共得到255个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为$\frac{1}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-5 | B. | -2x-1 | C. | -1 | D. | 5-2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 健康 | 非健康 | 总计 | |
| 经常参加体育锻炼 | p | ||
| 不参加体育锻炼 | q | 100 | |
| 总计 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com