
| ���� | �ǽ��� | �ܼ� | |
| ������������� | p | ||
| ����������� | q | 100 | |
| �ܼ� | 200 |
���� �������ö���չ��ʽ��ͨ�ʽ��������p��q��ֵ��
�����ɣ���p=40��q=10�������2��2�����������K2�����ٽ�ֵ�Ƚϣ����ɵó���99%�Ŀɿ���Ҫ������Ϊ�����彡���뾭���μ����������йء���
��� �⣺���ߣ�1+2x��5��չ��ʽͨ����Tr+1=C5r2rxr������1�֣�
��չ��ʽ�ĵ������ǣ�T2+1=C5222x2=40x2��
��������ϵ����p=40�� ����3�֣�
�֡�չ��ʽ�ĵ�����Ķ���ʽϵ��ΪC53��
��q=C53=10�� ����5�֣�
�����ɣ���p=40��q=10����
| ���� | �ǽ��� | �ܼ� | |
| ������������� | 40 | 60 | 100 |
| ����������� | 10 | 90 | 100 |
| �ܼ� | 50 | 150 | 200 |
���� ������Ҫ�������ʽ������Ӧ�ã�����ʽչ��ʽ��ͨ�ʽ�������Եļ��飬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $C_{10}^5$ | B�� | $C_{10}^5•{3^5}•{��{-2}��^5}$ | C�� | $C_{10}^4•{3^6}•{��{-2}��^4}$ | D�� | $C_{10}^4$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
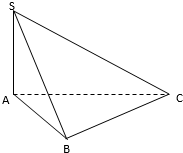 ��ͼ��������S-ABC�У�AC��BC��AC=3��BC=4��SA=SB=$\sqrt{13}$��ƽ��SAB��ƽ��ABC��������S-BC-A�Ĵ�СΪ��������
��ͼ��������S-ABC�У�AC��BC��AC=3��BC=4��SA=SB=$\sqrt{13}$��ƽ��SAB��ƽ��ABC��������S-BC-A�Ĵ�СΪ��������| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 31�� | B�� | 32�� | C�� | 34�� | D�� | 36�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1-\sqrt{3}}{4}$ | B�� | $\frac{\sqrt{3}-1}{4}$ | C�� | -$\frac{1}{2}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ϲ����ѧ�� | ��ϲ����ѧ�� | �ϼ� | |
| ���� | 60 | 20 | 80 |
| �� | 10 | 10 | 20 |
| �ϼ� | 70 | 30 | 100 |
| A�� | 4.762 | B�� | 9.524 | C�� | 0.0119 | D�� | 0.0238 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com