练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．复数z=$\frac{1+2i}{1-i}$对应的点z在复数平面的（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    分析 利用复数的运算法则、几何意义即可得出．

    解答 解：复数z=$\frac{1+2i}{1-i}$=$\frac{（1+2i）（1+i）}{（1-i）（1+i）}$=$\frac{-1+3i}{2}$对应的点z$（-\frac{1}{2}，\frac{3}{2}）$在复数平面的第二象限．
    故选：B．

    点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

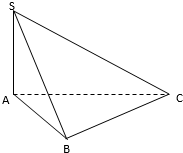    10．如图，在三棱锥S-ABC中，AC⊥BC，AC=3，BC=4，SA=SB=$\sqrt{13}$，平面SAB⊥平面ABC，则二面角S-BC-A的大小为（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知sin（π-θ）-cos（$\frac{π}{2}$+θ）=2$\sqrt{3}$cos（2π-θ），则sinθcosθ-cos2θ=（　　）
    A．$\frac{1-\sqrt{3}}{4}$B．$\frac{\sqrt{3}-1}{4}$C．-$\frac{1}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．某研究中心为研究运动与性别的关系得到2×2列联表如表：
    喜欢数学课不喜欢数学课合计
    男生602080
    女生101020
    合计7030100
    则随机变量K2的观测值约为（　　）
    A．4.762B．9.524C．0.0119D．0.0238

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．化简$\frac{{cos（π+α）cos（\frac{11π}{2}-α）}}{{cos（π-α）sin（\frac{9π}{2}+α）}}$，得到的结果是（　　）
    A．-sinαB．cosαC．-tanαD．-$\frac{cosα}{sinα}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．给出下列类比推理命题（其中Q为有理数集，R为实数集，C为复数集），其中类比结论错误的是（　　）
    A．“若a，b∈R，则a-b=0⇒a=b”类比推出“若a，b∈C，则a-b=0⇒a=b”．
    B．“若a，b∈R，则a-b＞0⇒a＞b”类比推出“若a，b∈C，则a-b＞0⇒a＞b”．
    C．“若a，b，c，d∈R，则复数a+bi=c+di⇒a=c，b=d”类比推出“若a，b，c，d∈Q，则实数a+$\sqrt{3}$b=c+$\sqrt{3}$d⇒a=c，b=d”
    D．“若a，b∈R，则|a+b|≤|a|+|b|”类比推出“若a，b∈C，则|a+b|≤|a|+|b|”．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．（x2+$\frac{1}{x^2}$+2）5展开式中x4项的系数为120．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设点P在椭圆x2+$\frac{{y}^{2}}{m}$=1上，点Q在直线y=x+4上，若|PQ|的最小值为$\sqrt{2}$，则m=$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知两个变量有比较好的线性相关关系，可以用回归直线来近似刻画它们之间的关系，关于回归直线的方程，有下述结论：
    ①回归方程只适用于我们所研究的样本的总体；
    ②建立的回归方程一般都有时间性；
    ③样本取值的范围会影响回归方程的适用范围．
    其中正确结论的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    同步练习册答案