练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知两个变量有比较好的线性相关关系，可以用回归直线来近似刻画它们之间的关系，关于回归直线的方程，有下述结论：
    ①回归方程只适用于我们所研究的样本的总体；
    ②建立的回归方程一般都有时间性；
    ③样本取值的范围会影响回归方程的适用范围．
    其中正确结论的个数为（　　）
    A．0B．1C．2D．3

    分析 根据回归方程的意义，对题目中的命题进行分析、判断即可．

    解答 解：对于①，回归方程只适用于我们所研究的样本的总体，不适用于一切样本和总体，命题正确；
    对于②，回归方程一般都有时间性，例如不能用20世纪80年代的身高、体重数据所建立的回归方程，
    描述现在的身高和体重的关系，命题正确；
    对于③，样本取值的范围会影响回归方程的适用范围；例如回归方程是由大人身高、体重数据所建立的，
    不能用它来描述幼儿时期的身高与体重的关系，命题正确；
    综上，正确命题的个数为3．
    故选：D．

    点评 本题考查回归分析的意义以及注意的问题．是对回归分析的思想、方法小结，要结合实例进行分析判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．复数z=$\frac{1+2i}{1-i}$对应的点z在复数平面的（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

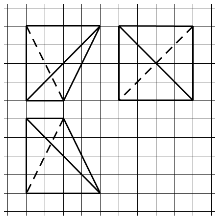    1．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体最长的棱长等于（　　）
    A．4B．6C．$4\sqrt{2}$D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设D为△ABC所在平面内一点，且$\overrightarrow{BD}$=3$\overrightarrow{CD}$，则（　　）
    A．$\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AC}$B．$\overrightarrow{AD}$=$\frac{4}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$C．$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AC}$D．$\overrightarrow{AD}$=-$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{2}$$\overrightarrow{AC}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在等腰直角三角形ABC中，已知AB=AC=1，E，F分别是边AB，AC上的点，且$\overrightarrow{AE}$=m$\overrightarrow{AB}$，$\overrightarrow{AF}$=n$\overrightarrow{AC}$，其中m，n∈（0，1）且m+2n=1，若EF，BC的中点分别为M，N，则|$\overrightarrow{MN}$|的最小值是$\frac{\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．为了解“网络游戏对当代青少年的影响”做了一次调查，共调查了26名男同学、24名女孩同学．调查的男生中有8人不喜欢玩电脑游戏，其余男生喜欢玩电脑游戏；而调查的女生中有9人喜欢玩电脑游戏，其余女生不喜欢电脑游戏．
    （1）根据以上数据填写如下2×2的列联表：
    性别
    对游戏态度    		男生女生合计
    喜欢玩电脑游戏18927
    不喜欢玩电脑游戏81523
    合计262450
    （2）根据以上数据，能否在犯错误的概率不超过0.025的前提下认为“喜欢玩电脑游戏与性别关系”？
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
    P（K2≥k0）0.050.0250.010
    k03.8415.0246.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设函数f′（x）是偶函数f（x）（x∈（-∞，0）∪（0，+∞）的导函数，f（-1）=0，当x＞0时，xf′（x）-f（x）＜0，则使得f（x）＞0成立的x的取值范围是（　　）
    A．（-∞，-1）∪（0，1）B．（-1，0）∪（1，+∞）C．（-1，0）∪（0，1）D．（0，1）∪（1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．双曲线$\frac{{x}^{2}}{64}$-$\frac{{y}^{2}}{36}$=1的离心率为（　　）
    A．$\frac{4}{5}$B．$\frac{5}{4}$C．$\frac{3}{4}$D．$\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

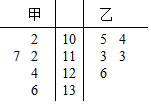    20．为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取5名学生的成绩作样本，如图是样本的茎叶图，规定：成绩不低于120分时为优秀成绩．
    （1）从甲班的样本中有放回的随机抽取2个数据，求其中只有一个优秀成绩的概率；
    （2）从甲、乙两个班级的样本中分别抽取2名学生的成绩，记获优秀成绩的总人数为X，求X的分布列．

    查看答案和解析>>

    同步练习册答案