
分析 (1)求出不等式的解集,根据对应关系求出m,n的值即可;(2)根据绝对值不等式的性质证明即可.
解答 解:(1)由|x-$\frac{1}{4}$|≤$\frac{1}{12}$得-$\frac{1}{12}$≤x-$\frac{1}{4}$≤$\frac{1}{12}$,
即$\frac{1}{6}$≤x≤$\frac{1}{3}$,
∵不等式|x-$\frac{1}{4}$|≤$\frac{1}{12}$的解集为{x|n≤x≤m},
∴n=$\frac{1}{6}$,m=$\frac{1}{3}$,
(2)证明:3|b|=|3b|=|2(a+b)-(2a-b)|≤2|a+b|+|2a-b|,
∵|a+b|<m,|2a-b|<n,∴|a+b|<$\frac{1}{3}$,|2a-b|<$\frac{1}{6}$,
则3|b|≤2|a+b|+|2a-b|<2×$\frac{1}{3}$+$\frac{1}{6}$=$\frac{5}{6}$,即|b|<$\frac{5}{18}$.
点评 本题考查了解绝对值不等式问题,考查绝对值的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩B=∅ | B. | ∁UA∪B=R | C. | A∩B=B | D. | A∪B=B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 49 54 43 54 15 37 17 93 39 78 87 35 20 96 43 84 17 34 91 64 |
| 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
| A. | 06 | B. | 17 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3-4\sqrt{3}}}{10}$ | B. | $\frac{{3+4\sqrt{3}}}{10}$ | C. | $\frac{{-3-4\sqrt{3}}}{10}$ | D. | $\frac{{-3+4\sqrt{3}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
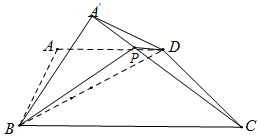 如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.
如图,已知等腰梯形ABCD中,AD∥BC,BC=2AD=2AB=4,将△ABC沿BD折到△A′BD的位置,使平面A′BD⊥平面CBD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com