
分析 化简极坐标方程为普通方程,求出双曲线和它的共轭双曲线的离心率分别为e1和e2,然后利用双曲线的性质探索e1和e2的关系.
解答 解:∵曲线$\left\{{\begin{array}{l}{x=asecα}\\{y=btanα}\end{array}}\right.$(α为参数)化为:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$,与曲线$\left\{{\begin{array}{l}{x=atanβ}\\{y=bsecβ}\end{array}}\right.$(β为参数)化为:$\frac{{y}^{2}}{{b}^{2}}-\frac{{x}^{2}}{{a}^{2}}=1$,e1=$\frac{c}{a}$,e2=$\frac{c}{b}$,$\frac{1}{{{e}_{1}}^{2}}$+$\frac{1}{{{e}_{2}}^{2}}$=$\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$=1,∴e1e2≥2,∴e1+e2≥2$\sqrt{{e}_{1}{e}_{2}}$=2$\sqrt{2}$.
故答案为:$2\sqrt{2}$.
点评 本题考查极坐标与普通方程的互化,考查双曲线的简单性质以及基本不等式的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
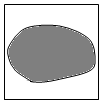 如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒100粒豆子,落在阴影区域内的豆子共60粒,据此估计阴影区域的面积为$\frac{12}{5}$.
如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒100粒豆子,落在阴影区域内的豆子共60粒,据此估计阴影区域的面积为$\frac{12}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=3x-3 | B. | y=$\frac{1}{3}$x-$\frac{1}{3}$ | C. | y=-$\frac{1}{3}$x+$\frac{1}{3}$ | D. | y=-3x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂直 | B. | 不垂直也不平行 | C. | 平行且同向 | D. | 平行且反向 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com