
| A. | (x-1)2+(y+1)2=1 | B. | (x+2)2+(y-2)2=1 | C. | (x+1)2+(y-1)2=1 | D. | (x-2)2+(y+2)2=1 |
分析 先求出圆x2+y2+2x-2y+1=0的圆心和半径;再利用两点关于已知直线对称所具有的结论,求出所求圆的圆心坐标即可求出结论.
解答 解:∵圆x2+y2+2x-2y+1=0转化为标准方程为(x+1)2+(y-1)2=1,
所以其圆心为:(-1,1),r=1,
设(-1,1)关于直线x-y+3=0对称点为:(a,b)
则有$\left\{\begin{array}{l}{\frac{a-1}{2}-\frac{1+b}{2}+3=0}\\{\frac{b-1}{a+1}×1=-1}\end{array}\right.$⇒$\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$.
故所求圆的圆心为:(-2,2).半径为1.
所以所求圆的方程为:(x+2)2+(y-2)2=1
故选:B.
点评 本题是基础题,考查对称圆的方程问题,重点在于求出对称圆的圆心坐标和半径,本题考查函数和方程的思想,注意垂直条件的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)设实数x,y满足不等式组$\left\{\begin{array}{l}|{x+y-6}|≤2\\ y≤2x+4≤4y+4\end{array}\right.$,作出不等式组表示的平面区域,并求当a>0时,z=y-ax的最大值;
(1)设实数x,y满足不等式组$\left\{\begin{array}{l}|{x+y-6}|≤2\\ y≤2x+4≤4y+4\end{array}\right.$,作出不等式组表示的平面区域,并求当a>0时,z=y-ax的最大值;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{80}{243}$ | B. | $\frac{13}{243}$ | C. | $\frac{4}{243}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
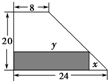 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x、y应为15,12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com