
| A. | 必要条件 | B. | 充分条件 | C. | 充要条件 | D. | 无关条件 |
分析 由题意看命题f(x)在x=x0处连续与命题f(x)在x=x0处有定义是否能互推,然后根据必要条件、充分条件和充要条件的定义进行判断,
由“函数f(x)在点x=x0处连续”可得“函数f(x)在点x=x0处有极限”.通过举反例可得由“函数f(x)在点x=x0处有极限”,不能推出“函数f(x)在点x=x0处连续”,由此得出结论.
解答 解:由f(x)在点x=x0处连续的定义,可知f(x)在点x=x0处连续⇒函数f(x)在点x=x0处有定义;
反之不成立.故为必要而不充分的条件,
由“函数f(x)在点x=x0处连续”可得“函数f(x)在点x→x0处有极限”.
但由“函数f(x)在点x→x0处有极限”,不能推出“函数f(x)在点x=x0处连续”,
例如f(x)=$\left\{\begin{array}{l}{x,x>0}\\{2,x=0}\\{-x,x<0}\end{array}\right.$在x→0处有极限为0,但f(x)在x=0处不连续.
故“函数f(x)在点x=x0处连续”是“函数f(x)在点x→x0处有极限”的充分而不必要条件,
故函数f(x)在点x0处有定义,是当x→x0时f(x)有极限的无关条件,
故选:D.
点评 本题主要考查充分条件、必要条件、充要条件的定义和判断方法,函数在某点连续与函数在某点有极限的关系,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
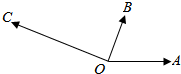 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}⊥\overrightarrow{OC}$,设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别为( )| A. | x=-2,y=-1 | B. | x=-2,y=1 | C. | x=2,y=-1 | D. | x=2,y=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com